Question

How do you evaluate arctan (-1) using a unit circle?

Answer 1

Hint: It is clearly understood that we need to do all the calculation part using a circle and that too with a unit circle where obviously we take radius as 1 in the defined unit. Arctan (-1) obviously we know that we want to evaluate the inverse of tangent function at -1.

Complete step-by-step answer:
We will use the unit circle that is a circle of radius 1 which will have its centre at origin which is (0,0) and here the tangent of theta angle that is $\tan (\theta )$ is the y coordinate value divided by the x coordinate value of the intersection of the unit circle and a ray which is extending from the origin making an angle theta.

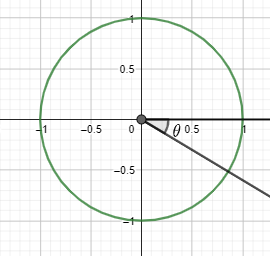
Now finding the inverse of tangent at -1 or arctan (-1) is the same as evaluating for theta in $\tan \theta $ =-1.
This will happen when x and y have equal magnitudes or values what we normally say but have the opposite signs within the defined domain of theta as $\theta \in [0,2\pi ]$ and this happens only at some particular values of theta.
And as per the requirement of the question we get this case true only when $\theta =\dfrac{3\pi }{4}$ and will also be true when $\theta =\dfrac{7\pi }{4}$ .

Note: We must be aware of the angles and signs that we need to take for particular angles as the value of the functions differ with signs obviously. Also we must remember the rotation and signs we take for various trigonometric angles.