Question

How do you evaluate $\sec \left( -\dfrac{\pi }{6} \right)$ ?

Answer 1

Hint: We have to find the value of a negative angle of the secant function which is a trigonometric function. We shall use basic trigonometry to analyze the angle that has been referred to and then find its value in the secant function. For this, we must know the values of secant of the few principal angles in trigonometry derived by using the Pythagorean theory.

Complete step by step answer:
When we move in the anti-clockwise direction in the coordinate plane, the angles measured in this direction are all positive. However, when we move in the clockwise direction in the coordinate plane, the angles measured in this direction are considered to be all negative. Therefore, the negative angle given in the problem signifies that it has been measured in the clockwise sense.
We understand that $-\dfrac{\pi }{6}$ lies in the fourth quadrant of the cartesian plane which consists of angles ranging from $\left( \dfrac{3\pi }{2},2\pi \right)$ in the anticlockwise sense and angles ranging from $\left( 0,-\dfrac{\pi }{2} \right)$ in the clockwise sense.
According to the cartesian rule of sign of trigonometric functions, all the values of secant of angles lying in the fourth quadrant are positive.

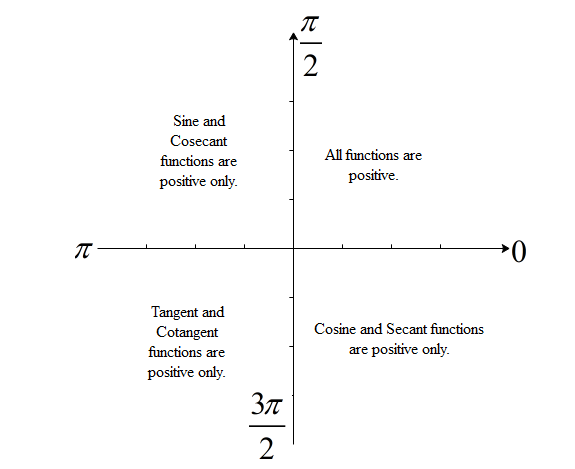
This implies that $\sec \left( -\dfrac{\pi }{6} \right)$ must have a positive value. Thus, it can be written as $\sec \left( \dfrac{\pi }{6} \right)$.
Now, by the basic values of trigonometric functions, we know that $\sec \left( \dfrac{\pi }{6} \right)=\dfrac{2}{\sqrt{3}}$.
$\Rightarrow \sec \left( -\dfrac{\pi }{6} \right)=\dfrac{2}{\sqrt{3}}$

Therefore, the value of $\sec \left( -\dfrac{\pi }{6} \right)$ is $\dfrac{2}{\sqrt{3}}$.

Note: In the cartesian plane, the angles follow a particular sign system. According to this, all the trigonometric functions are positive in the first quadrant, only sine and cosecant functions are positive in the second quadrant, only tangent and cotangent functions are positive in the third quadrant and only cosine and secant functions are positive in the fourth quadrant.