Question

Evaluate the following
\[{{\cot }^{2}}{{30}^{o}}-2{{\cos }^{2}}{{60}^{o}}-\dfrac{3}{4}{{\sec }^{2}}{{45}^{o}}-4{{\sec }^{2}}{{30}^{o}}\]

Answer 1

Hint:First of all, consider the expression given in the question. Now make the table for trigonometric ratios of general angles. Now, from that find the values of \[\cot {{60}^{o}},sec{{45}^{o}},\sec {{30}^{o}}\] and \[\cot {{30}^{o}}\] and substitute these in the given expression to get the required answer.

Complete step-by-step answer:
In this question, we have to find the value of the expression
\[{{\cot }^{2}}{{30}^{o}}-2{{\cos }^{2}}{{60}^{o}}-\dfrac{3}{4}{{\sec }^{2}}{{45}^{o}}-4{{\sec }^{2}}{{30}^{o}}\]
Let us consider the expression given in the question.
\[E={{\cot }^{2}}{{30}^{o}}-2{{\cos }^{2}}{{60}^{o}}-\dfrac{3}{4}{{\sec }^{2}}{{45}^{o}}-4{{\sec }^{2}}{{30}^{o}}...\left( i \right)\]
Now, we have to find the values of \[\sec {{45}^{o}},\cos {{60}^{o}},\sec {{30}^{o}}\] and \[\cot {{30}^{o}}\].
Let us make the table for trigonometric ratios of general angles like \[{{0}^{o}},{{30}^{o}},{{45}^{o}},{{60}^{o}},{{90}^{o}}\] and find the required values.

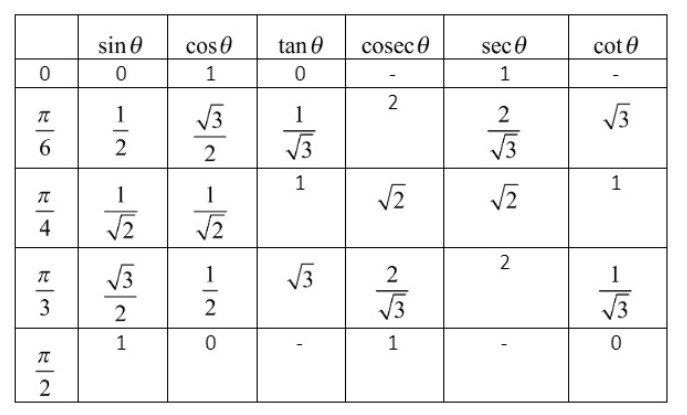
From the above table, we get, \[\cot {{30}^{o}}=\sqrt{3}\]. By substituting this in equation (i), we get,
\[E={{\left( \sqrt{3} \right)}^{2}}-2{{\cos }^{2}}{{60}^{o}}-\dfrac{3}{4}{{\sec }^{2}}{{45}^{o}}-4{{\sec }^{2}}{{30}^{o}}\]
Also from the above table, we get \[\cos {{60}^{o}}=\dfrac{1}{2}\]. By substituting this in the above equation, we get, \[E={{\left( \sqrt{3} \right)}^{2}}-2{{\left( \dfrac{1}{2} \right)}^{2}}-\dfrac{3}{4}{{\sec }^{2}}{{45}^{o}}-4{{\sec }^{2}}{{30}^{o}}\]
From the table, we also get, \[\sec {{45}^{o}}=\sqrt{2}\]. By substituting this in the above equation, we get,
\[E={{\left( \sqrt{3} \right)}^{2}}-2{{\left( \dfrac{1}{2} \right)}^{2}}-\dfrac{3}{4}{{\left( \sqrt{2} \right)}^{2}}-4{{\sec }^{2}}{{30}^{o}}\]
From the table, we also get, \[\sec {{30}^{o}}=\dfrac{2}{\sqrt{3}}\]. By substituting this in the above equation, we get,
\[E={{\left( \sqrt{3} \right)}^{2}}-2{{\left( \dfrac{1}{2} \right)}^{2}}-\dfrac{3}{4}{{\left( \sqrt{2} \right)}^{2}}-4{{\left( \dfrac{2}{\sqrt{3}} \right)}^{2}}\]
By simplifying the above equation, we get,
\[E=3-2\left( \dfrac{1}{4} \right)-\dfrac{3}{4}\left( 2 \right)-4\left( \dfrac{4}{3} \right)\]
\[E=3-\dfrac{2}{4}-\dfrac{6}{4}-\dfrac{16}{3}\]
\[E=\dfrac{3}{1}-\dfrac{1}{2}-\dfrac{3}{2}-\dfrac{16}{3}\]
\[E=\dfrac{18-3-9-32}{6}\]
\[E=\dfrac{18-44}{6}\]
\[E=\dfrac{-26}{6}\]
\[E=\dfrac{-13}{3}\]
Hence, we get the value of the expression \[{{\cot }^{2}}{{30}^{o}}-2{{\cos }^{2}}{{60}^{o}}-\dfrac{3}{4}{{\sec }^{2}}{{45}^{o}}-4{{\sec }^{2}}{{30}^{o}}\] as \[\dfrac{-13}{3}\].

Note: In these types of questions, students must take care of the calculation that should be done according to the BODMAS rule. Also, students are advised to memorize at least the values of \[\sin \theta \] and \[\cos \theta \] at different angles and from these values, they can find all the other trigonometric ratios like in the above question, they can find \[\cot {{30}^{o}}\] by using \[\dfrac{\cos {{30}^{o}}}{\sin {{30}^{o}}},\sec {{45}^{o}}\] by \[\dfrac{1}{\cos {{45}^{o}}}\] and \[\sec {{30}^{o}}\] by \[\dfrac{1}{\cos {{30}^{o}}}\].