
Explain positive, negative and zero work. Give one example of each.
Answer
521.4k+ views
2 likes
Hint: Write formula of work
Dot product of two component A and B
Where
Find
Complete step by step answer:
The work done by a force on a particle during a displacement is given as
Here, W = work
Positive work done – The work done is said to be positive when force and displacement are in the same direction.
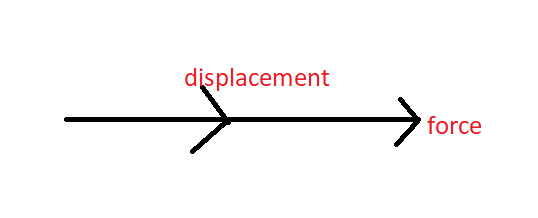
Hence, work is positive.
Zero work – the work done is said to be zero when force and displacement are perpendicular to each other.
Hence, work is zero
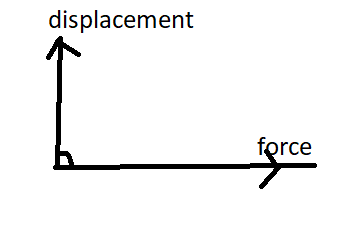
Negative work done – The work done is said to be negative when force and displacement are in opposite directions.
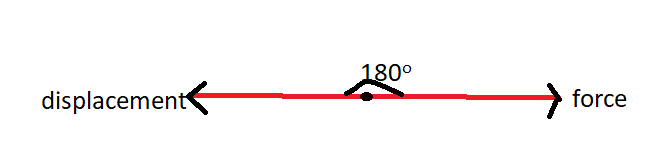
Hence, work is negative.
Note: Work done by friction is always zero because friction force and displacement act in opposite directions. When a spring travels from A to B and from B back to A then work done during the return journey is negative of the work during the onwards journey and the net work done by the spring is zero.
Dot product of two component A and B
Where
Find
Complete step by step answer:
The work done by a force on a particle during a displacement is given as
Here, W = work
Positive work done – The work done is said to be positive when force and displacement are in the same direction.

Hence, work is positive.
Zero work – the work done is said to be zero when force and displacement are perpendicular to each other.
Hence, work is zero

Negative work done – The work done is said to be negative when force and displacement are in opposite directions.

Hence, work is negative.
Note: Work done by friction is always zero because friction force and displacement act in opposite directions. When a spring travels from A to B and from B back to A then work done during the return journey is negative of the work during the onwards journey and the net work done by the spring is zero.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




