
Explain series connections of Resistors and derive the formula of equivalent resistance.
Answer
478.2k+ views
1 likes
Hint: Resistor is an electrical component that is used to convert the current into the voltage or the voltage into the current. Resistors are said to be in series when they are connected in one line. Here, we will use ohm’s law to calculate the formula of equivalent resistance.
Complete step by step answer:
Consider a circuit carrying a current
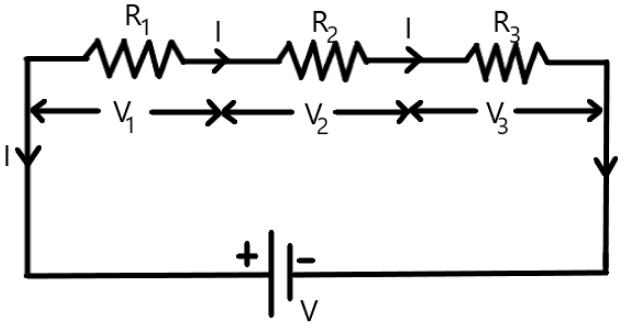
Here,
Now, as the resistors are connected in series, the current flowing through the circuit will be the same across all the resistors. Now, the voltage
Now, if a resistor
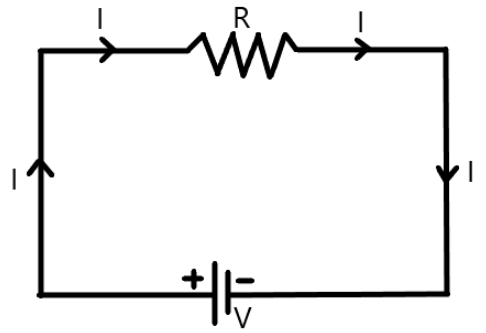
Therefore, for an equivalent resistance,
Now, the voltage drop across the resistance
The voltage drop across the resistance
The voltage drop across the resistance
Therefore, the voltage
Now, taking
Now, as we know
Therefore,
Therefore, the above equation becomes
Which is the equivalent resistance.
Thus, we can say that the equivalent resistance
Note:All the resistors in the series do not get a source voltage, therefore, they divide the voltage across them. Also, the amount of energy used by the resistors will be the same as the amount of energy used by a single resistor. This energy is also divided across the resistors depending upon their resistances.
Complete step by step answer:
Consider a circuit carrying a current

Here,
Now, as the resistors are connected in series, the current flowing through the circuit will be the same across all the resistors. Now, the voltage
Now, if a resistor

Therefore, for an equivalent resistance,
Now, the voltage drop across the resistance
The voltage drop across the resistance
The voltage drop across the resistance
Therefore, the voltage
Now, taking
Now, as we know
Therefore,
Therefore, the above equation becomes
Which is the equivalent resistance.
Thus, we can say that the equivalent resistance
Note:All the resistors in the series do not get a source voltage, therefore, they divide the voltage across them. Also, the amount of energy used by the resistors will be the same as the amount of energy used by a single resistor. This energy is also divided across the resistors depending upon their resistances.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




