Question

Explain \[s{p^3}d\] hybridization by taking a suitable example.

Answer 1

Hint: to explain hybridization one should know the concepts of steric number and the details of that molecule such as the lone pair and the number and types of bonds present in the molecule.

Complete step by step solution:
\[s{p^3}d\] hybridization consists of one ‘s’, three ‘p’ and one ‘d’ orbitals. They are almost of the same energy which are intermixed to give 5 identical and degenerate hybrid orbitals. They are arranged in trigonal bipyramidal symmetry.
To explain their symmetry-

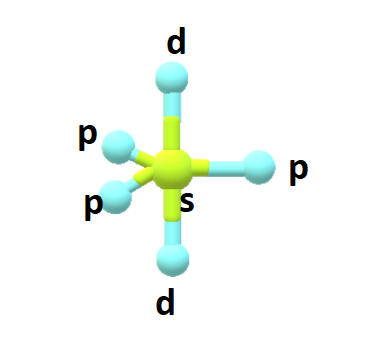
Amongst the five degenerate hybrid orbitals ,three of them are arranged in a trigonal plane and the remaining two orbitals are present above and below the trigonal plane at right angles.
Percentage (%) of s , p , d characters in the molecule-
The \[s{p^3}d\] hybrid orbitals consist of 20% ‘s’,60% ‘p’ and 20% ‘d’ characters.
For example-
The \[PC{l_5}\]molecule has five orbitals i.e. 1s,3p and 1d are intermixed to get 5 degenerate hybrid orbitals \[s{p^3}d\] of the same energy. They are directed to the 5 corners of the trigonal bipyramidal. All the bond angles in trigonal bipyramidal are not identical.
In \[PC{l_5}\] molecules the five hybrid orbitals of phosphorus overlap with p orbitals of chlorine atoms. The p orbitals of the molecule are singly occupied. Together they form 5 \[P - Cl\] sigma bonds.
The Equatorial bonds-
The 3 \[P - Cl\] bonds which lie in the trigonal plane make an angle with one another. The angle between them is \[{120^ \circ }\].
Axial bonds-
The 2 \[P - Cl\] bonds where one lies above the equatorial plane and the other below make an angle of \[{90^ \circ }\] with the plane.

Note: Students often consider the pie bonds during the calculation of hybridization. But it is only the sigma bonds which participate. One should keep in mind that different hybridisation provides the different way of arrangement in the space.