Question

Explain the Heisenberg Uncertainty Principle, and how the interpretation of it changes from the quantum to classical limits?

Answer 1

Hint: The Heisenberg uncertainty principle was given by the German physicist Werner Heisenberg in the year $ 1927 $ . This principle is one of the most important principles of Quantum Mechanics. This principle states that for the particle which behaves like both particle as well as wave, it will not be possible to accurately determine both the position and velocity at the same time.

Complete answer:
According to the Heisenberg Uncertainty Principle, if the uncertainty in the position of a wave-particle is small, the uncertainty in its momentum is large.
 $ \Delta x\Delta {p_x} \geqslant \dfrac{\hbar }{2} $
Mathematically, we could see that,
 $ \Delta x \to 0 $ , $ \Delta p \to \infty $ , so that
 $ \Delta x\Delta {p_x} \geqslant \dfrac{\hbar }{2} $
The Heisenberg Uncertainty Principle only applies to quantum objects like electrons and photons. Anything which is ordinarily-size has undetectable wave characteristics.

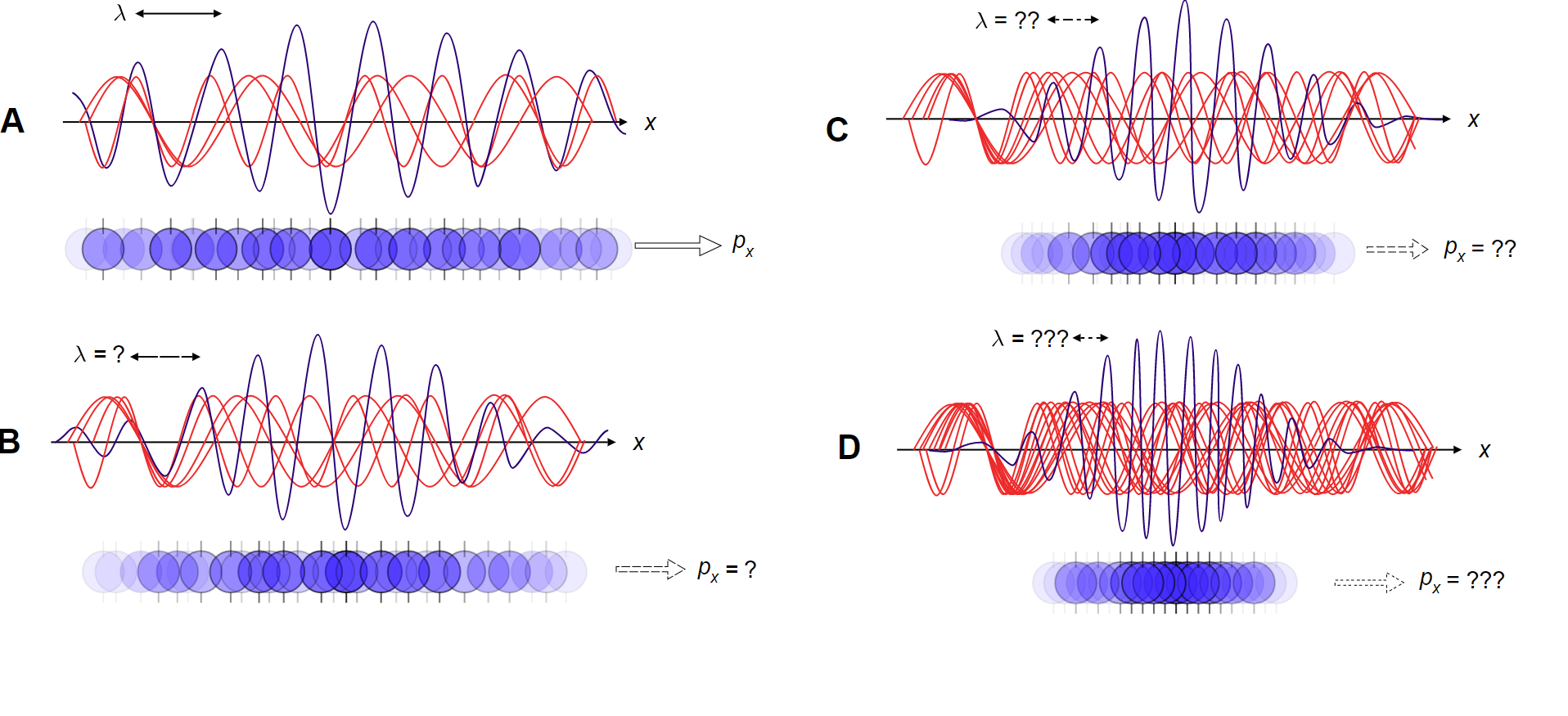
As we can see in the above image, in A; the wavelengths are well-defined. The momentum can be obtained from the wavelength, and so the momentum is also well-defined. $ \Delta x $ is larger and $ \Delta {p_x} $ is smaller. As while going from A to D, the value $ \Delta x \downarrow $ and $ \Delta {p_x} \uparrow $ . This is because for more assurance about position, we built a wave out of many super positions, taking advantage of the correspondence principle.
The correspondence principle states that in the limit as we stack more waves on the top of each other, ultimately the wavelengths become so small that the energy spectrum becomes continuous and we reach the classical limit, in which position is well-known.
Although, by doing this, we have layered so many waves that we have muddled them up amongst each other. Thus, we end up having a difficult time to refine the momentum via the wavelength.

Note:
If the position of the particles is the same, there would be an error in the momentum or the velocity or vice-versa. In the same way, the measurement of the momentum accurately will change the position. Thus, it proved that we cannot determine both position and momentum simultaneously.