Question

Explain why a rectangle is a convex quadrilateral.

Answer 1

Hint: A convex quadrilateral is a quadrilateral which has all interior angles less than 180 degrees and all the diagonals lie within the quadrilateral.

Complete step-by-step answer:
First, we look at a case where a quadrilateral is not convex. This would help in differentiating between a convex and non-convex quadrilateral.

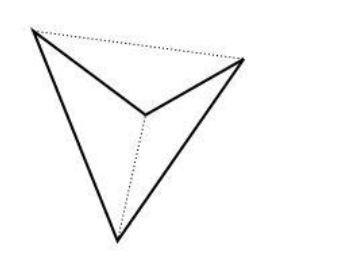
The above quadrilateral is non-convex. This is because it violates the definition since, one of the internal angles in this figure would be greater than 180 degrees. Further, if we draw various diagonals of the quadrilateral, one of the diagonals would lie outside the quadrilateral. (diagonals are marked in dashed lines) Thus this would be an example of convex quadrilateral.
Now, we will see why the rectangle is in fact a convex quadrilateral figure. In the case of a rectangle, we see (in the below figure) that all the interior angles are 90 degrees (thus less than 180 degrees).

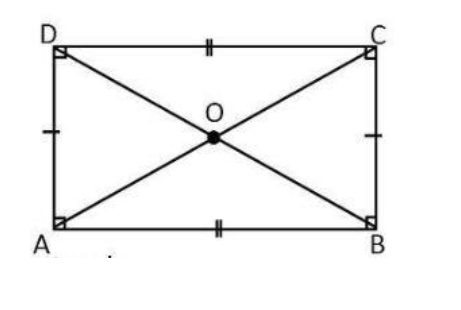
Further, all the diagonals are perpendicular bisectors and lie inside the quadrilateral (as shown above). Thus since, both the conditions of the definition are met for the case of a rectangle, we can conclude that it is a convex quadrilateral.
Note: In general, to check whether any polygon (for any figure with any number of sides) is convex or not non-convex, all we have to do is draw all the diagonals inside the polygon. Next, if this criterion is met, we check for every interior angle inside the polygon. If all the angles are less than 180 degrees, then the polygon is convex.