Question

Family of lines represented by the equation $\left( \cos \theta +\sin \theta \right)x+\left( \cos \theta -\sin \theta \right)y-3\left( 3\cos \theta +\sin \theta \right)=0$ passes through fixed point $M$ for all real value of $\theta $. Find $M$
A. $\left( 6,3 \right)$
B. $\left( 3,6 \right)$
C. $\left( -6,2 \right)$
D. $\left( 3,-6 \right)$

Answer 1

Hint: We will simplify the given family of lines and convert the given equation in the form of ${{L}_{1}}+\lambda {{L}_{2}}$. We know that the point of intersection of the lines can be given by solving ${{L}_{1}}=0$ and ${{L}_{2}}=0$.

Complete step-by-step answer:
Given that, family of curves represented by $\left( \cos \theta +\sin \theta \right)x+\left( \cos \theta -\sin \theta \right)y-3\left( 3\cos \theta +\sin \theta \right)=0$
Using multiplication distributive law i.e. $a\left( b+c \right)=ab+ac$ in the above equation then we will get
$\begin{align}
  & \left( \cos \theta +\sin \theta \right)x+\left( \cos \theta -\sin \theta \right)y-3\left( 3\cos \theta +\sin \theta \right)=0 \\
 & \Rightarrow x\cos \theta +x\sin \theta +y\cos \theta -y\sin \theta -9\cos \theta -3\sin \theta =0 \\
\end{align}$
Rearranging the terms in the above equation so that all the $\cos \theta $ terms at one place and the all the $\sin \theta $ terms are at one place.
$\Rightarrow \left( x\cos \theta +y\cos \theta -9\cos \theta \right)+\left( x\sin \theta -y\sin \theta -3\sin \theta \right)=0$
Now taking $\cos \theta $ common from the first term and $\sin \theta $ from the second term, then we will have
$\left( x+y-9 \right)\cos \theta +\left( x-y-3 \right)\sin \theta =0$
Dividing the above equation with $\cos \theta $ then we will get
$\begin{align}
  & \left( x+y-9 \right)\dfrac{\cos \theta }{\cos \theta }+\left( x-y-3 \right)\dfrac{\sin \theta }{\cos \theta }=\dfrac{0}{\cos \theta } \\
 & \Rightarrow \left( x+y-9 \right)+\tan \theta \left( x-y-3 \right)=0 \\
\end{align}$
Comparing the above equation with the family of line ${{L}_{1}}+\lambda {{L}_{2}}=0$, then we will have
${{L}_{1}}=x+y-9$
${{L}_{2}}=x-y-3$
We know that the point of intersection of the family of line ${{L}_{1}}+\lambda {{L}_{2}}=0$ can be given by solving ${{L}_{1}}=0$ and ${{L}_{2}}=0$.
$\therefore $ solving $x+y-9=0$ and $x-y-3=0$.
Value of $y$ from $x-y-3=0$ is given by $y=x-3$.
Substituting the value of $y$ from $x-y-3=0$ in the equation $x+y-9=0$, then we will get
$\begin{align}
  & x+y-9=0 \\
 & \Rightarrow x+\left( x-3 \right)-9=0 \\
 & \Rightarrow x+x-3-9=0 \\
\end{align}$
We know that $a+a=2a$ then
$2x-12=0$
Adding $12$ on both sides of the above equation, then we will have
$2x-12+12=0+12$
We know that $a-a=0$, then
$\Rightarrow 2x=12$
Dividing the above equation with $2$ on both sides of the equation, then
$\begin{align}
  & \Rightarrow \dfrac{2x}{2}=\dfrac{12}{2} \\
 & \Rightarrow x=6 \\
\end{align}$
Now the value of $y$ is $y=x-3=6-3=3$.
$\therefore $Point of intersection of the family of lines is $\left( x,y \right)=\left( 6,3 \right)$.
Option – A is correct answer.

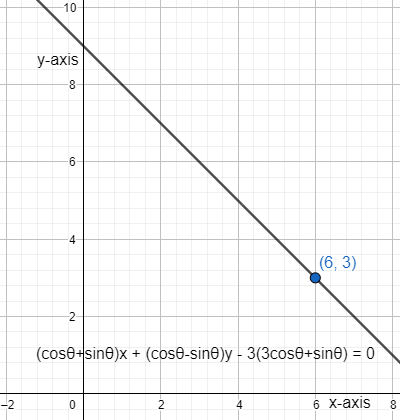
So, the correct answer is “Option A”.

Note: We can solve the equations $x+y-9=0$ and $x-y-3=0$ by adding both of them, then we will get
$\begin{align}
  & x+y-9+\left( x-y-3 \right)=0+0 \\
 & \Rightarrow x+y-9+x-y-3=0 \\
\end{align}$
Using $a+a=2a$, $a-a=0$ at a time in the above equation, then we will have
$\begin{align}
  & \Rightarrow 2x-12=0 \\
 & \Rightarrow 2x=12 \\
 & \Rightarrow x=6 \\
\end{align}$
Now the value of $y$ from $x+y-9=0$ can be calculated by substituting the value of $x=6$, then
$\begin{align}
  & x+y-9=0 \\
 & \Rightarrow 6+y-9=0 \\
 & \Rightarrow y-3=0 \\
 & \Rightarrow y=3 \\
\end{align}$
From both the methods we got the same answer.