
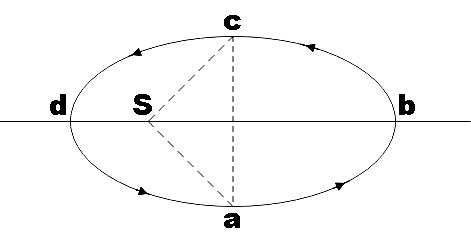
Figure shows elliptical path
A.
B.
C.
D.

Answer
480.3k+ views
3 likes
Hint: As a first step you could recall Kepler’s second law of planetary motion. Now you could find the area swept by the planet for traveling from
Complete step by step answer:
Figure shows elliptical path
In the question, we are given an elliptical path
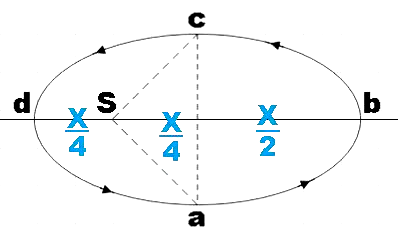
Let the total area of the ellipse be X, then the area of the triangle marked in the given figure will be,
We have a semi-ellipse
Now, let us recall Kepler’s second law. This law states that the imaginary line connecting a planet and the sun sweeps out equal areas in equal interval of time or simply, areal velocity of the planet around the sun is a constant, that is,
From the figure,
Substituting (2) and (3) in (1), we get,
Therefore, we found the required relation to be
So, the correct answer is “Option C”.
Note: Other than the law used in solving this question, we have two other Kepler’s laws for planetary motion. The first law is called the law of elliptical orbit which states that every planet moves around in an elliptical orbit with the sun at one of its focus. Then the other law is called the law of harmonics which states that the square of the time period of a planet is directly proportional to the cube of its orbital radius.
Complete step by step answer:
Figure shows elliptical path
In the question, we are given an elliptical path
Let the total area of the ellipse be X, then the area of the triangle marked in the given figure will be,
We have a semi-ellipse

Now, let us recall Kepler’s second law. This law states that the imaginary line connecting a planet and the sun sweeps out equal areas in equal interval of time or simply, areal velocity of the planet around the sun is a constant, that is,
From the figure,
Substituting (2) and (3) in (1), we get,
Therefore, we found the required relation to be
So, the correct answer is “Option C”.
Note: Other than the law used in solving this question, we have two other Kepler’s laws for planetary motion. The first law is called the law of elliptical orbit which states that every planet moves around in an elliptical orbit with the sun at one of its focus. Then the other law is called the law of harmonics which states that the square of the time period of a planet is directly proportional to the cube of its orbital radius.
Latest Vedantu courses for you
Grade 6 | CBSE | SCHOOL | English
Vedantu 6 Pro Course (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




