Question

Figures I, II, III and IV depict the variation of force with time. In which situation, the impulse will be maximum?

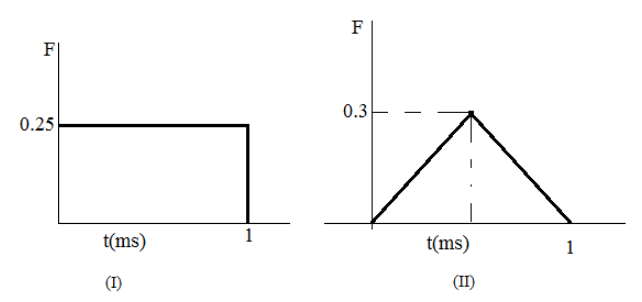
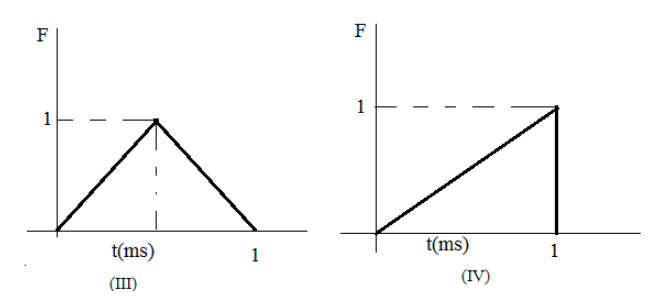
(A) I and II
(B) III and I
(C) III and IV
(D) Only IV

Answer 1

Hint: In this question, we need to determine the graph (out of the given four graphs) which will give the maximum impulse. For this, we will use the relation between the impulse, force and time.

Complete step by step answer:
The product of the force and time for which the force has been applied is known as the impulse. Mathematically, $I = Ft$.
Here, the plots have been given for Force vs Time. So, to determine the impulse, we have to evaluate the area under each of the curves and compare the results for the maximum impulse.
(I)For the first plot, the curve given resembles a rectangle with 0.25 as the width and 1ms as the length. The area of the rectangle is given as the product of the length and the width of the rectangle. So, the impulse for the curve is given as:
$
\Rightarrow I = Ft \\
\Rightarrow I = 0.25 \times 1 \\
\Rightarrow I = 0.25 \\
 $
(II) For the second plot, the curve given resembles a triangle which can be bifurcated into two right-angle triangles with 0.5 as the base and 0.3 as the height. The area of the right-angle triangle is given as half of the product of the base and the height of the triangle. So, the impulse for the curve is given as:
$
\Rightarrow I = Ft \\
\Rightarrow I = 2\left( {\dfrac{1}{2} \times b \times h} \right) \\
\Rightarrow I = 2\left( {\dfrac{1}{2} \times 0.5 \times 0.3} \right) \\
 \Rightarrow I = 0.15 \\
 $
(III) For the third plot, the curve given resembles a triangle which can be bifurcated into two right-angle triangles with 0.5 as the base and 1 as the height. The area of the right-angle triangle is given as half of the product of the base and the height of the triangle. So, the impulse for the curve is given as:
$
\Rightarrow I = Ft \\
\Rightarrow I = 2\left( {\dfrac{1}{2} \times b \times h} \right) \\
\Rightarrow I = 2\left( {\dfrac{1}{2} \times 0.5 \times 1} \right) \\
\Rightarrow I = 0.5 \\
 $
(IV) For the fourth plot, the curve given resembles a right-angle triangle with 1 as the base and 1 as the height. The area of the right-angle triangle is given as half of the product of the base and the height of the triangle. So, the impulse for the curve is given as:
$
\Rightarrow I = Ft \\
\Rightarrow I= \left( {\dfrac{1}{2} \times b \times h} \right) \\
\Rightarrow I= \left( {\dfrac{1}{2} \times 1 \times 1} \right) \\
\Rightarrow I= 0.5 \\
$
Hence, we can say that the impulse is maximum for the curves (III) and (IV) with the equivalent value of 0.5.

Hence,option C is correct.

Note:The area under the curve can be calculated by bifurcating the plot into small parts and then adding all the parts to get the resultant area. Impulse is the integral of the force over the change in the time period.