
Fill in the blanks.
Figure Center of rotational Order of rotational Angle of rotational Square Rectangle Rhombus Equilateral triangle Regular hexagon Circle Semi-circle
| Figure | Center of rotational | Order of rotational | Angle of rotational |
| Square | |||
| Rectangle | |||
| Rhombus | |||
| Equilateral triangle | |||
| Regular hexagon | |||
| Circle | |||
| Semi-circle |
Answer
557.4k+ views
Hint: We will take each shape of all diagrams and rotate them with suitable angles and find the angle of symmetry and the order of the symmetry. We need to know about the center of rotation, order of rotation and Angle of rotation.
Complete step-by-step answer:
For Square: -
We will consider a square and take the position of a vertex $p$ of the square in order to distinguish the position of the square. We are going to rotate the square $90{}^\circ $ as shown in below
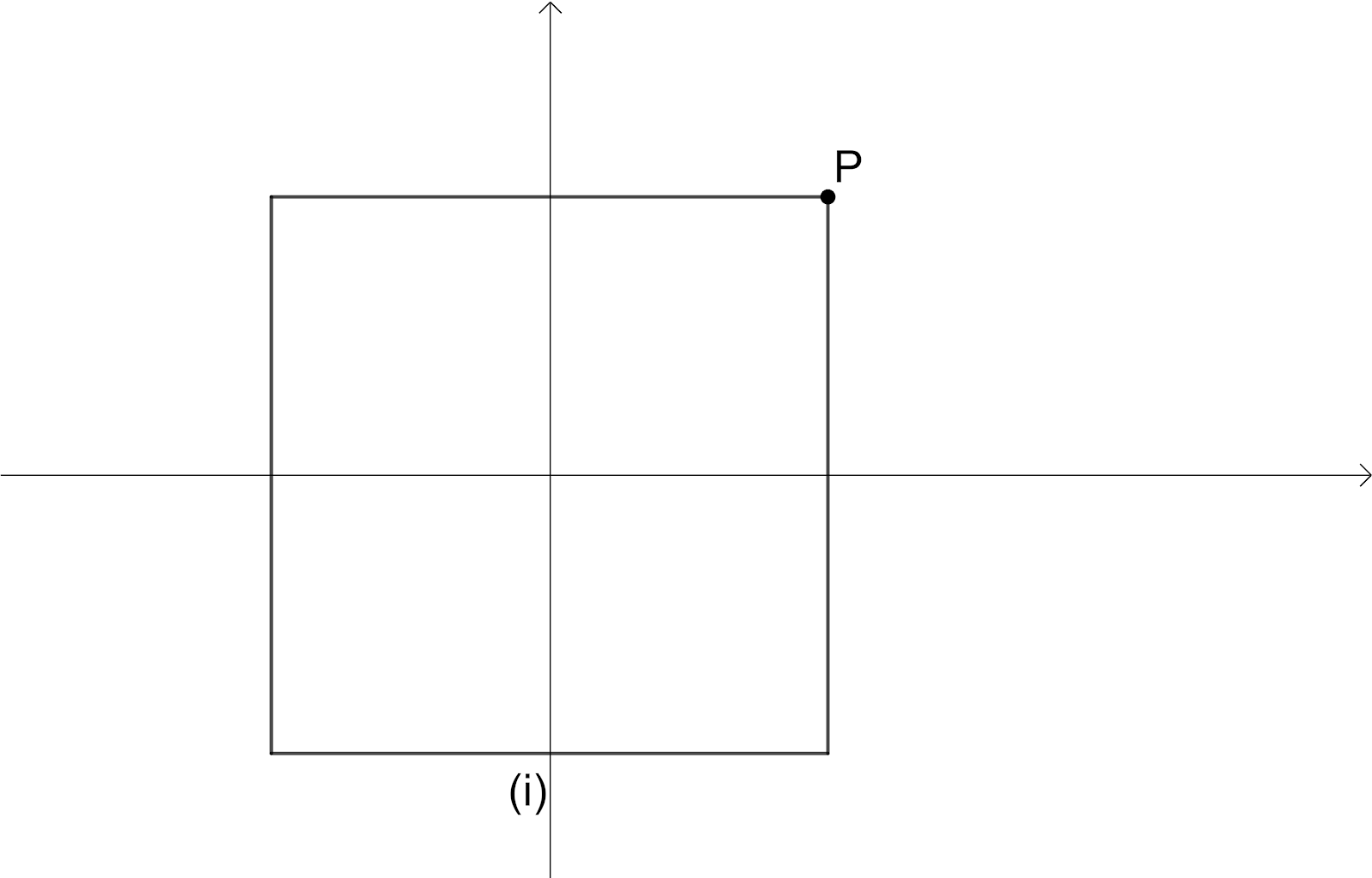
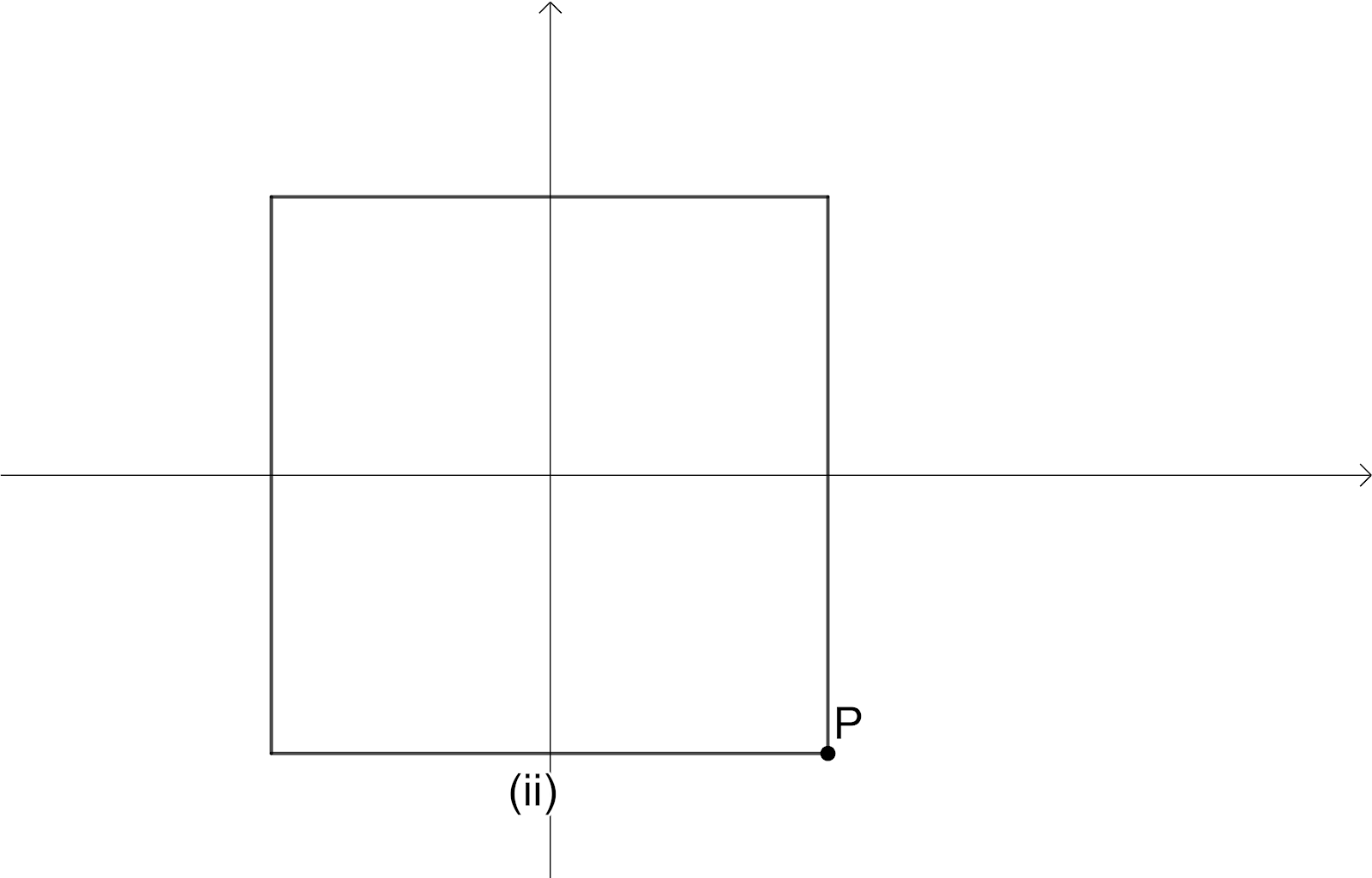
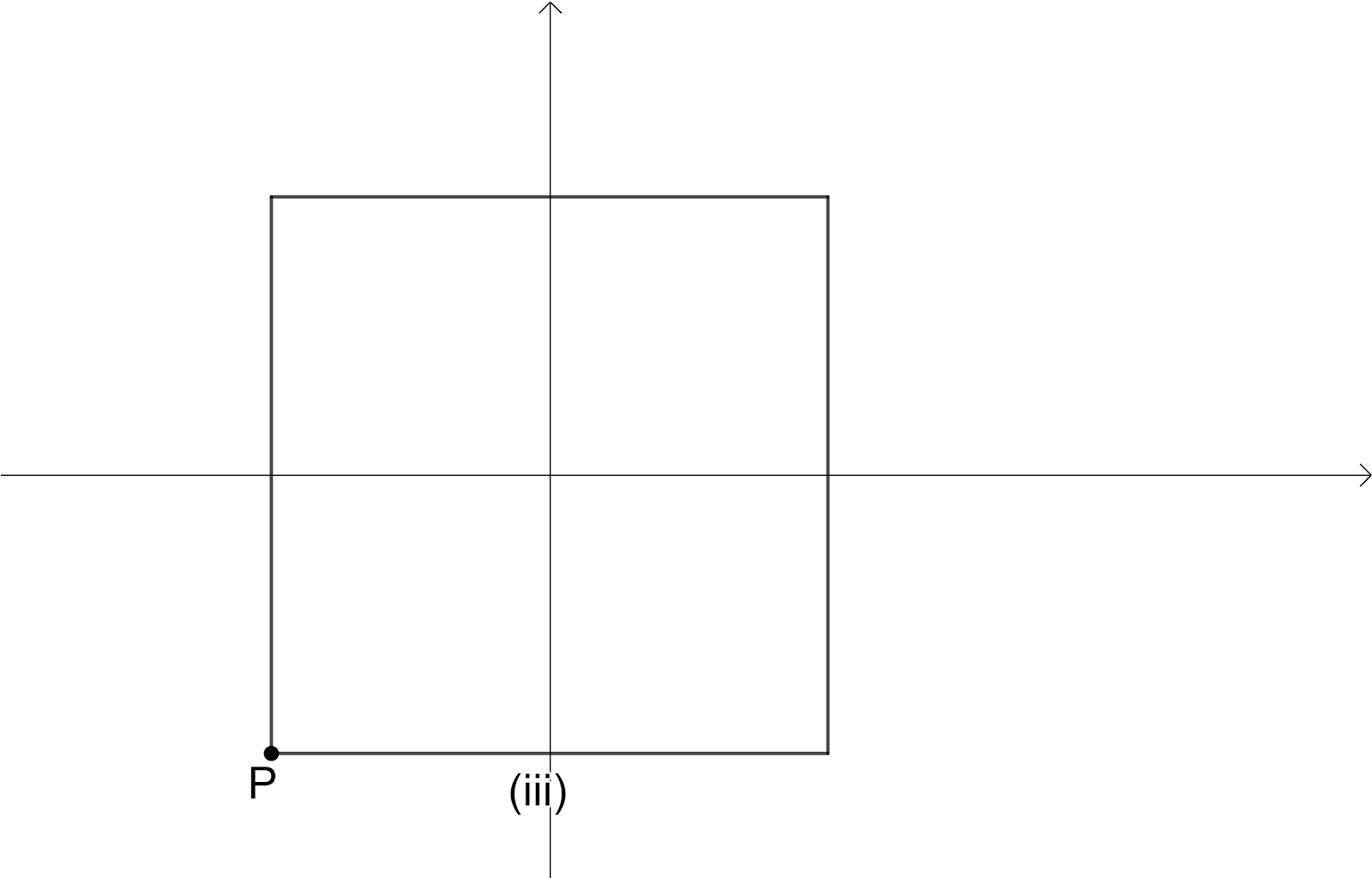
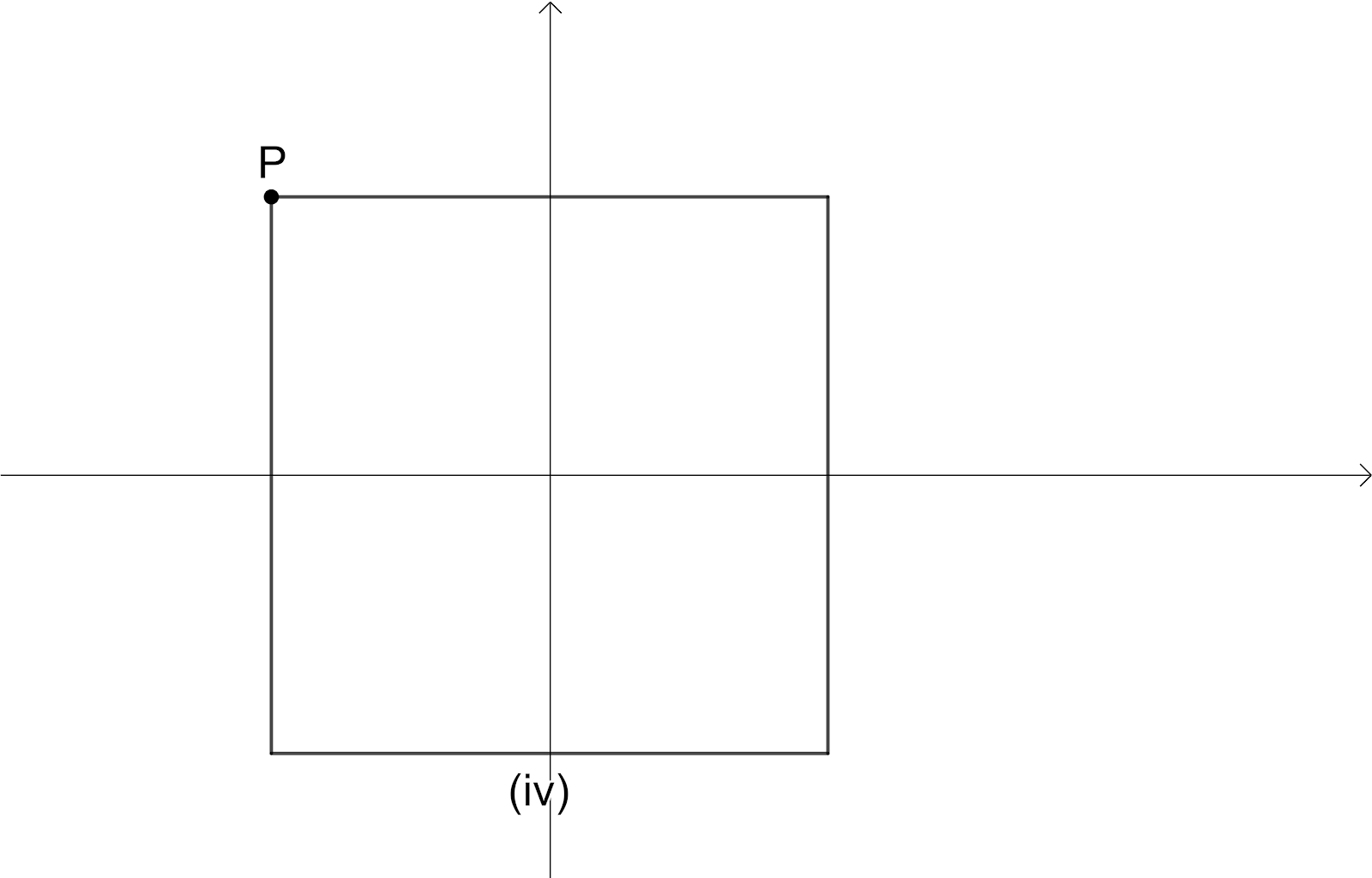
Here we have Intersection point of diagonals as Centre of the Rotation, the angle of rotation is $90{}^\circ $, The order of the rotational symmetry is $4$.
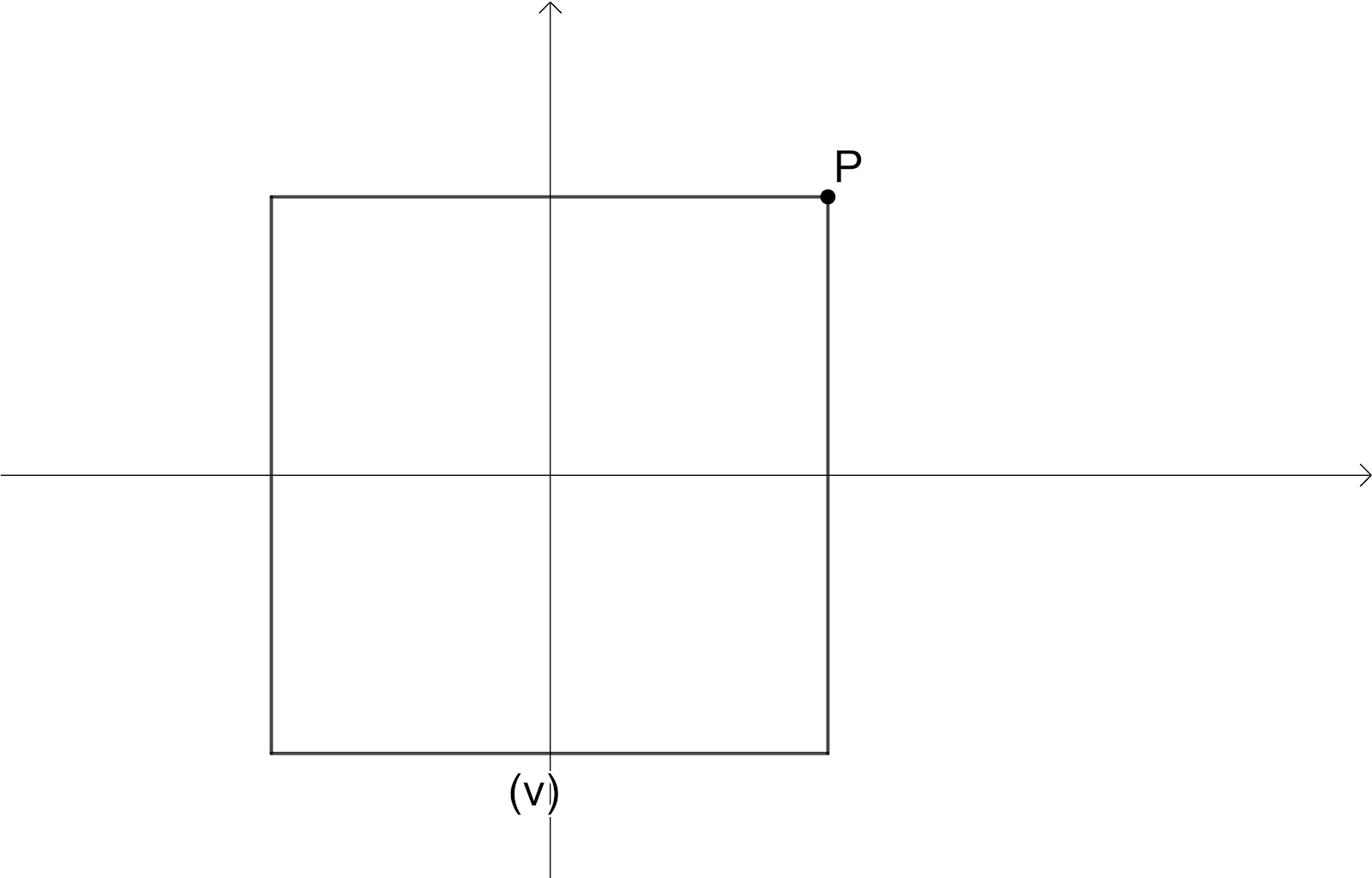
For Rectangle: -
We will consider a rectangle and we will rotate the rectangle $90{}^\circ $ as shown in figure.
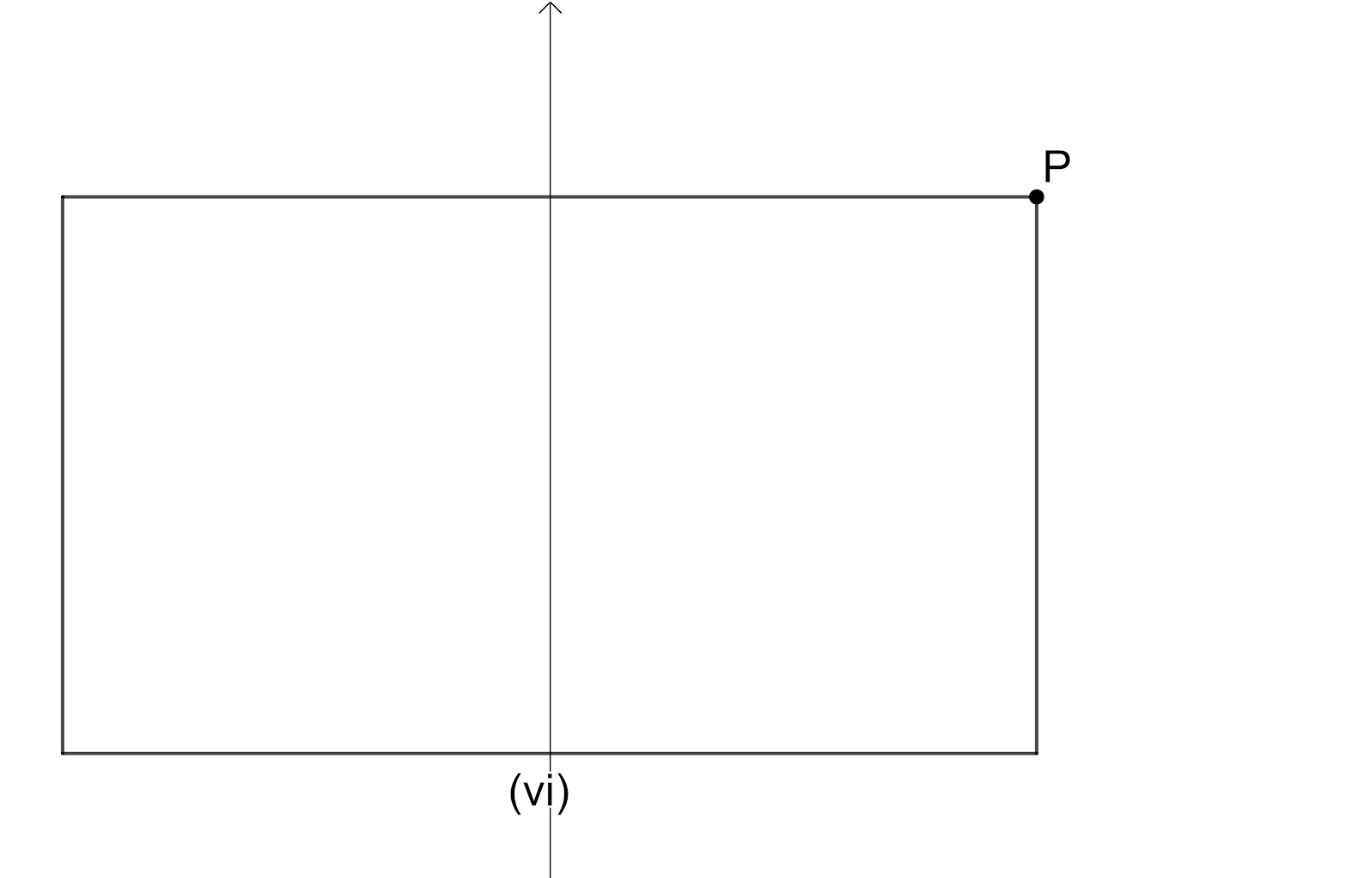
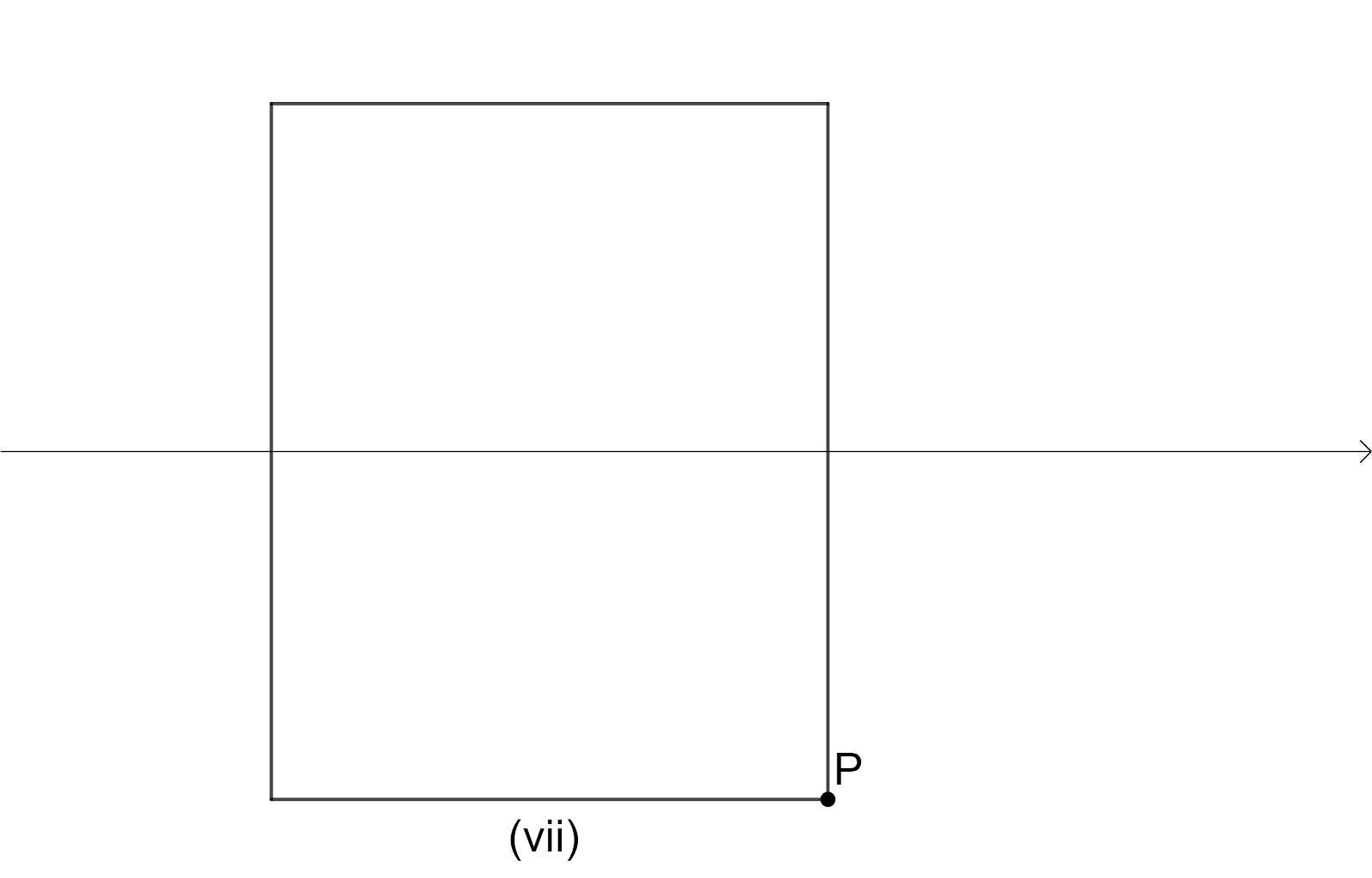
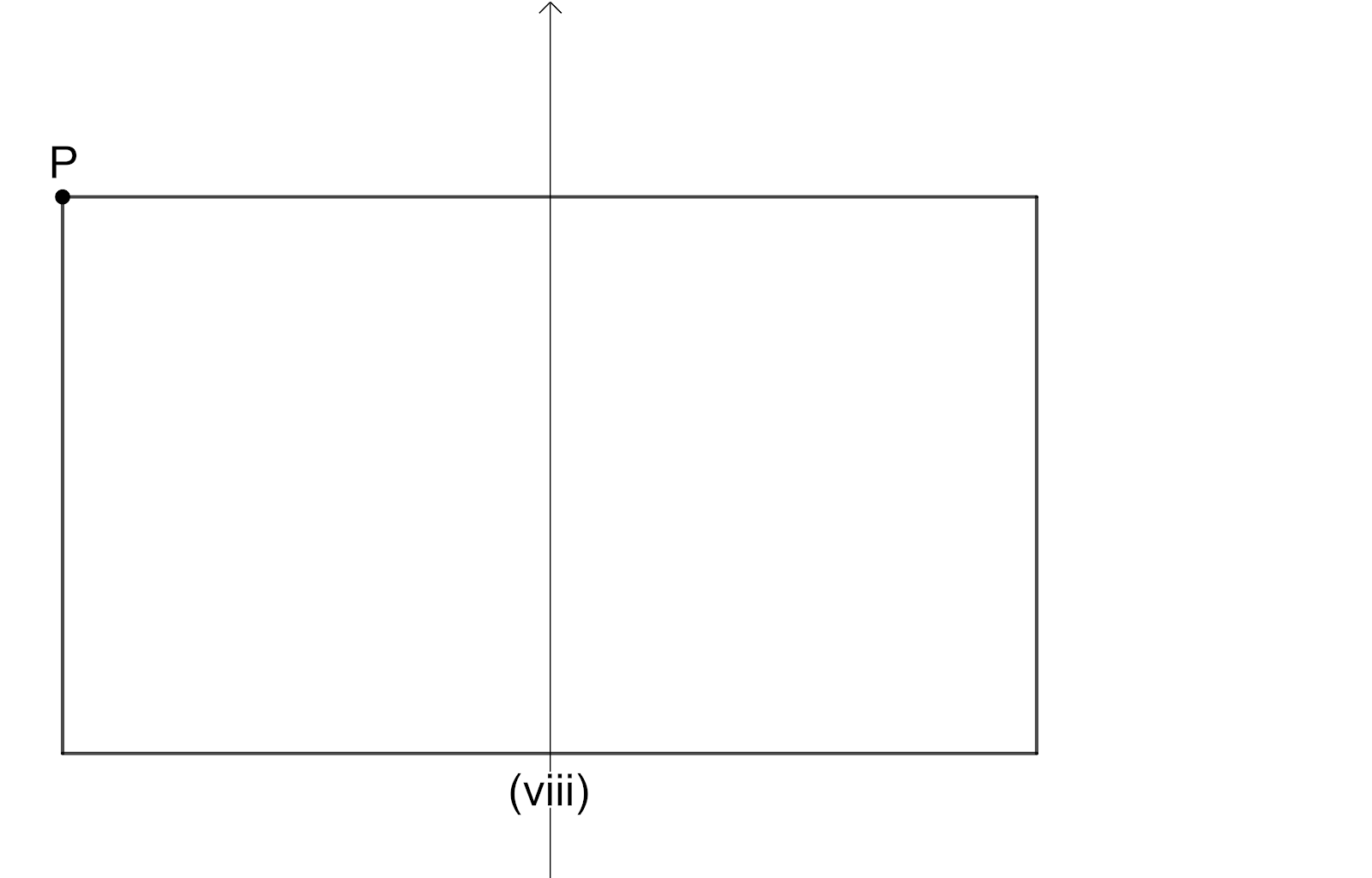
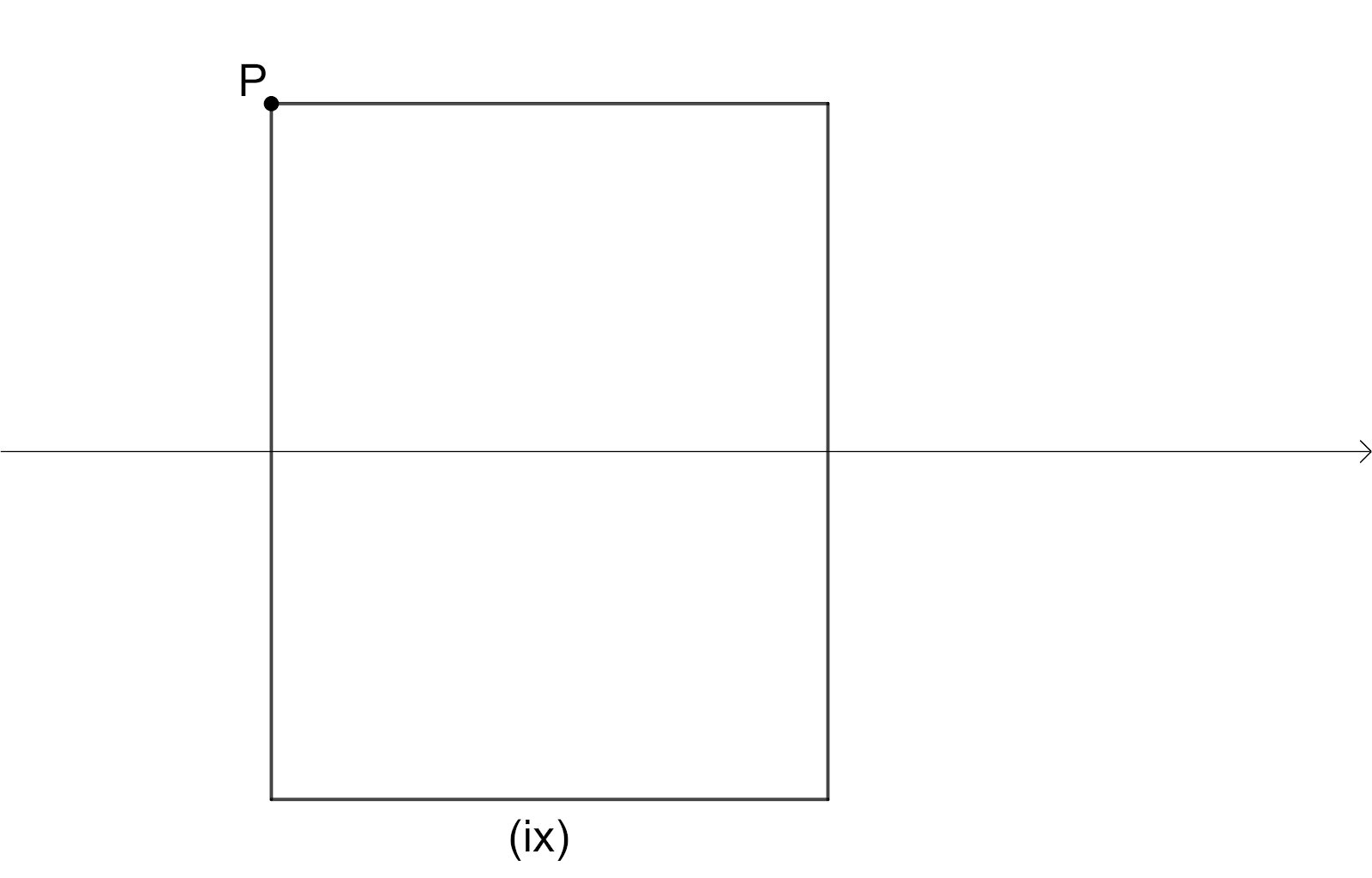
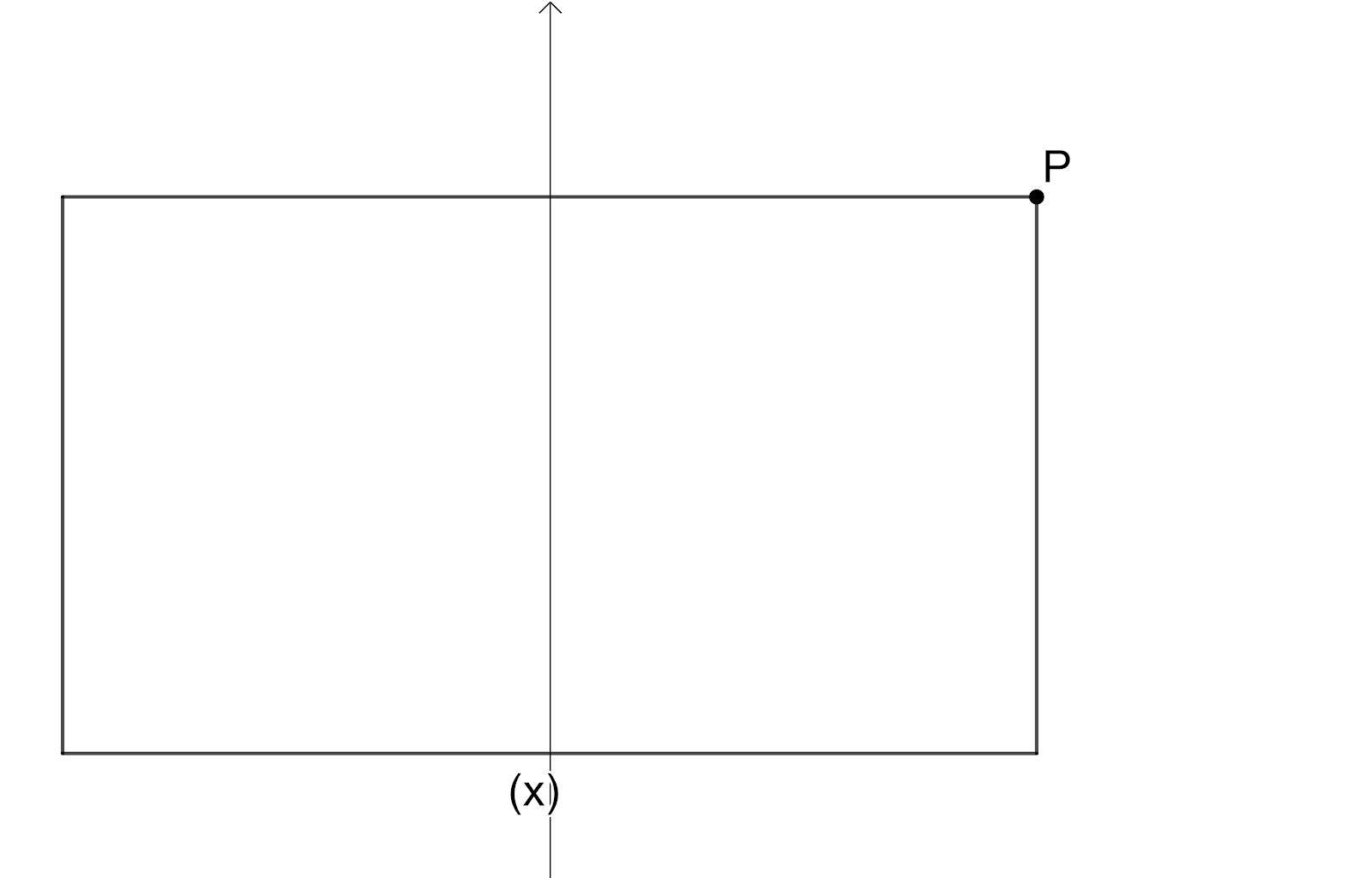
Here we have intersection point of the diagonals as Centre of the Rotation, the angle of rotation is $180{}^\circ $ since we have the original shape of rectangle when it is rotated $180{}^\circ $, The order of the rotational symmetry is $2$ since we get the original shape of rectangle $2$times.
For Rhombus: -
Rotate the rhombus $90{}^\circ $ then we have,
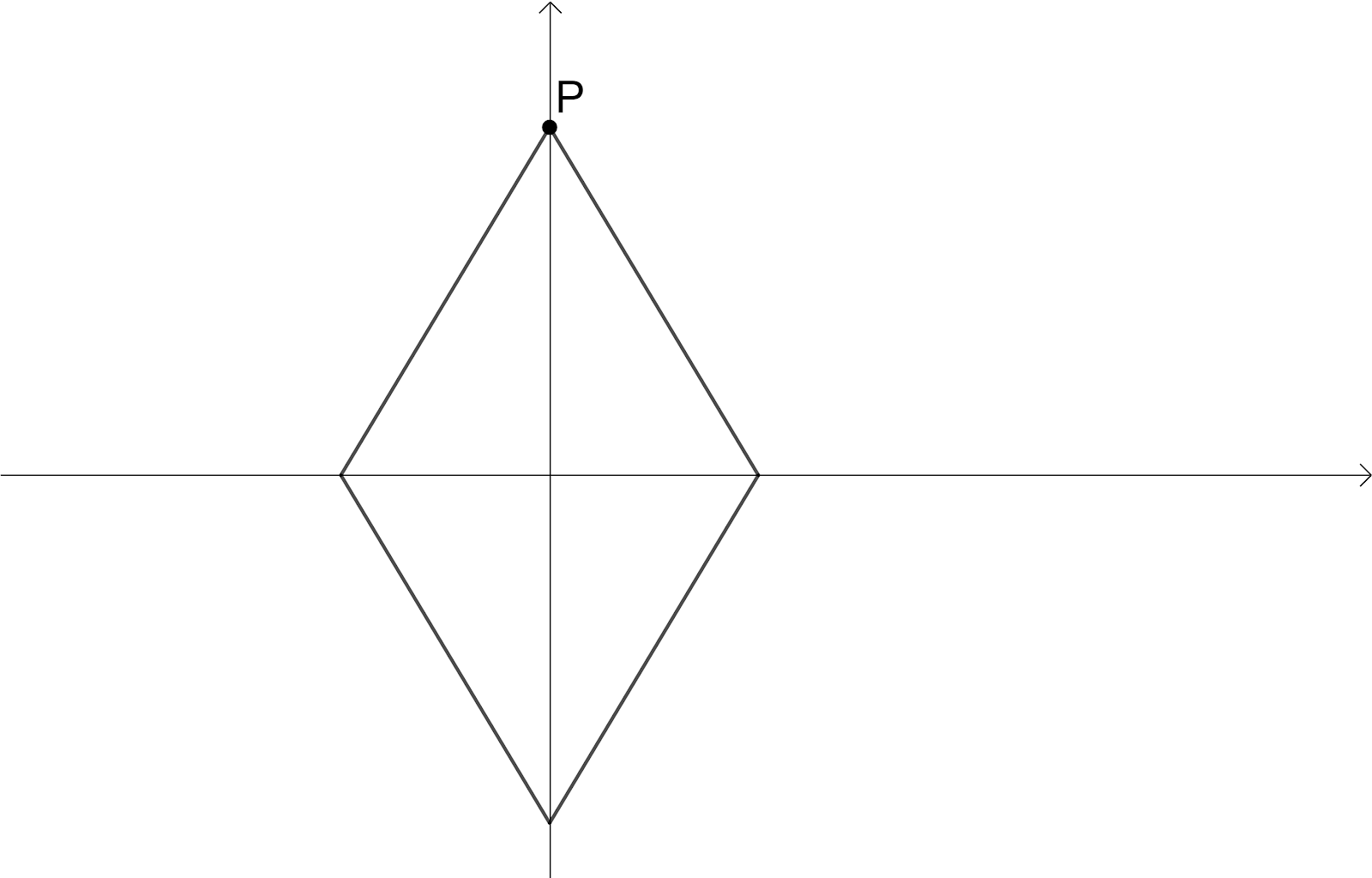
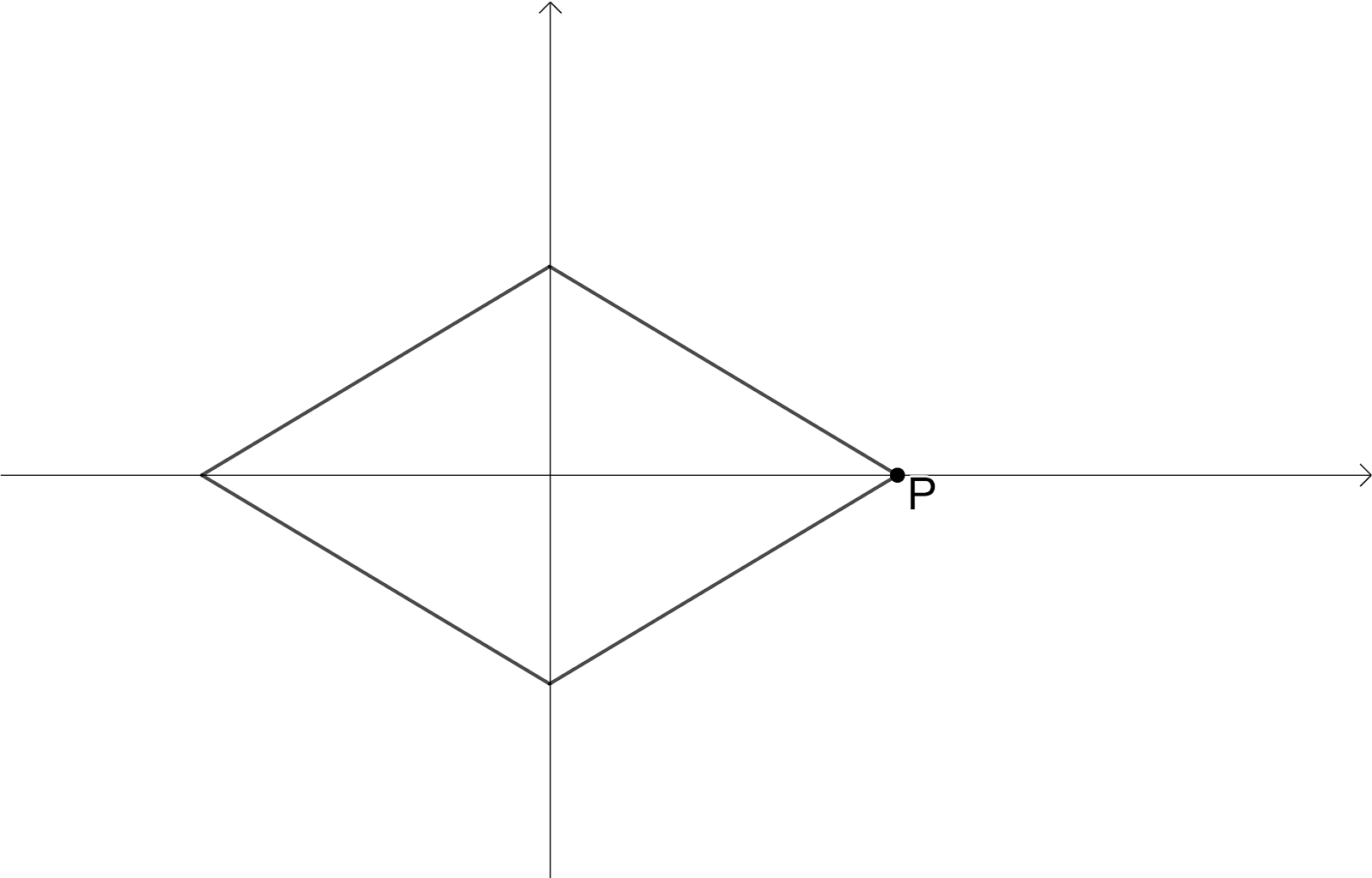
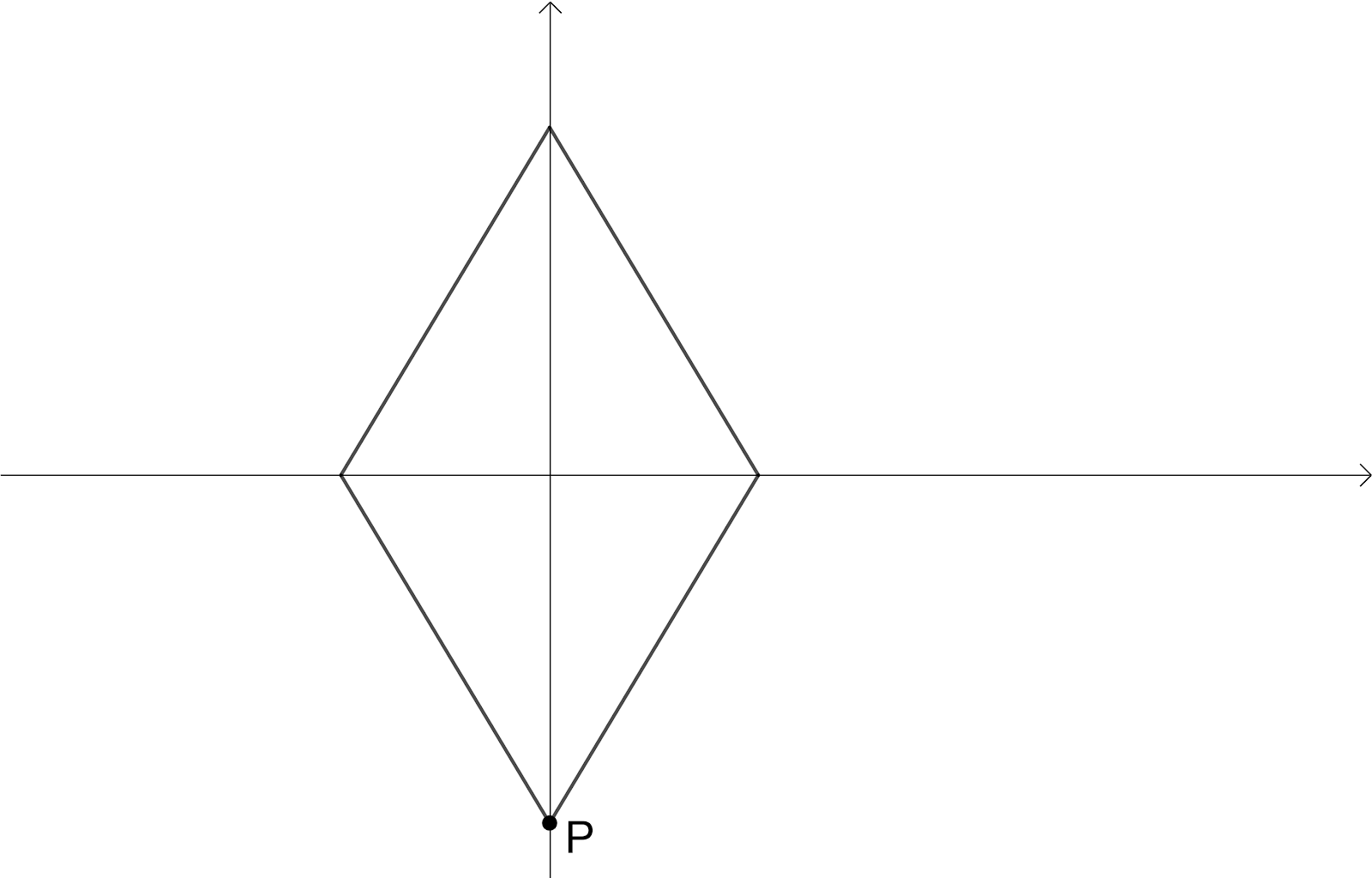
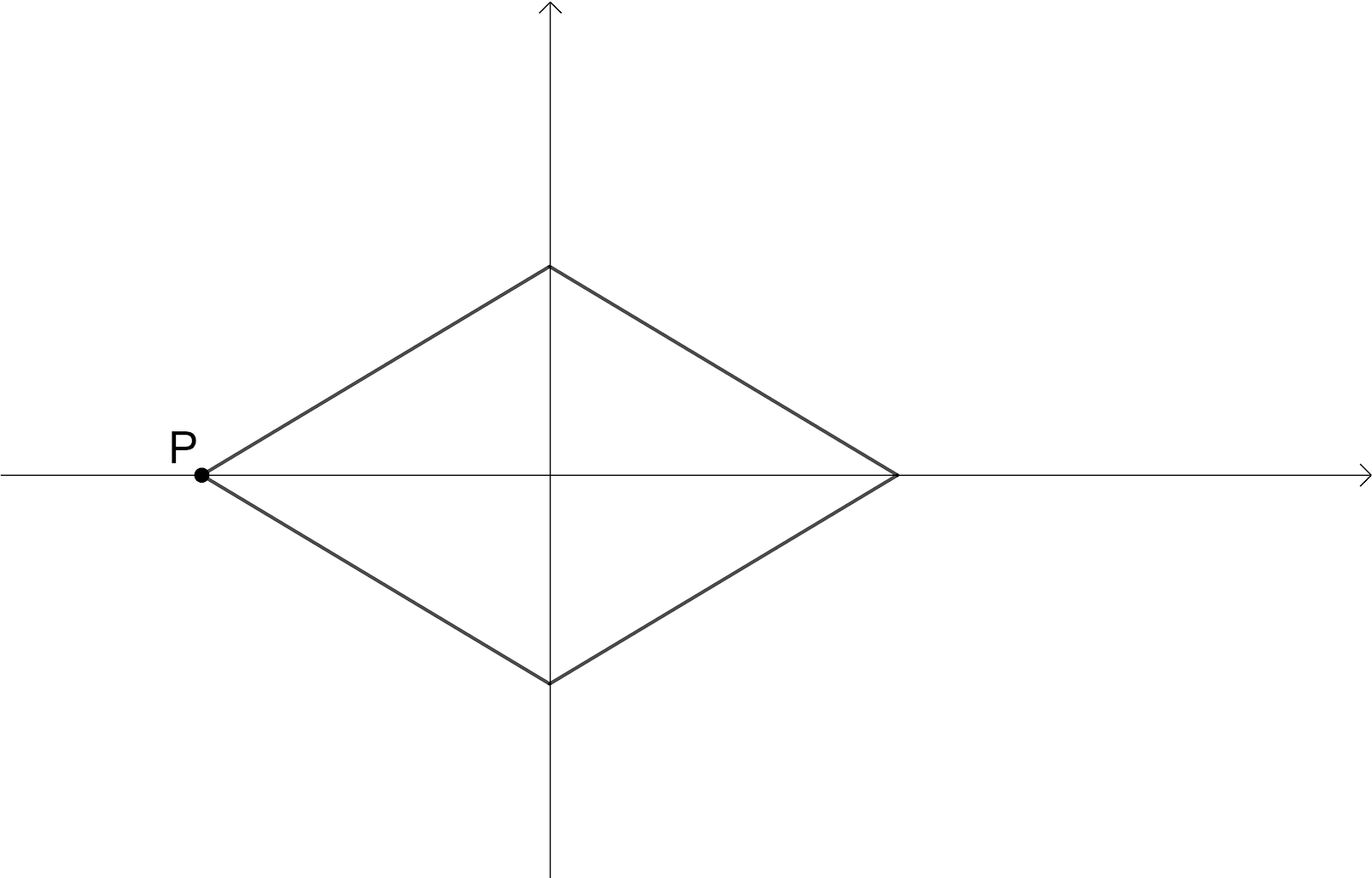
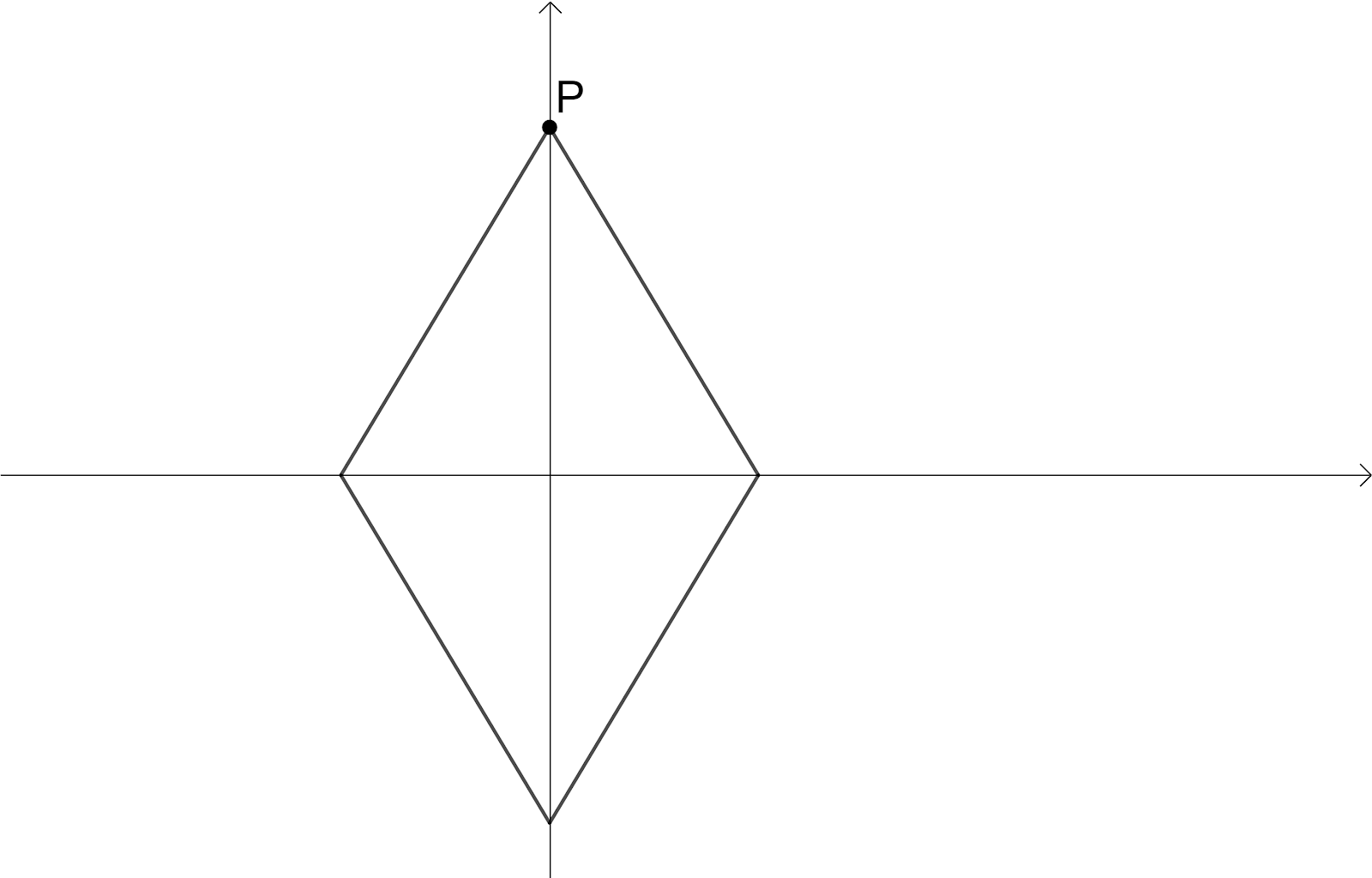
Here we have intersection point of the diagonals as Centre of the Rotation, the angle of rotation is $180{}^\circ $ since we have the original shape of rhombus when it is rotated $180{}^\circ $, The order of the rotational symmetry is $2$ since we get the original shape of rhombus $2$times.
For Equilateral Triangle: -
Take an equilateral triangle and rotate it $120{}^\circ $, then we have
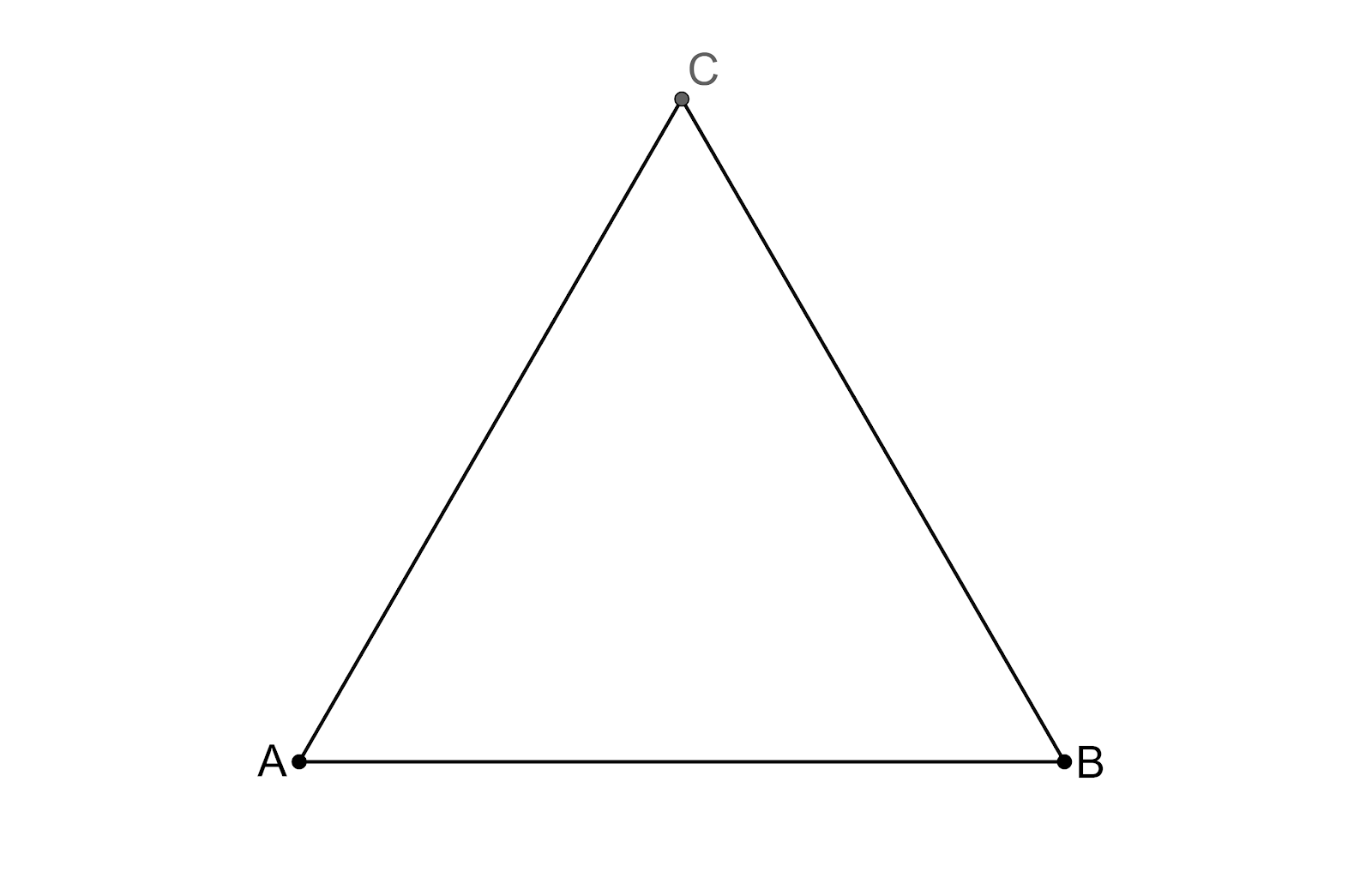
Here we have intersection point of medians as Centre of the Rotation, the angle of rotation is $120{}^\circ $ since we have the original shape of equilateral triangle when it is rotated $120{}^\circ $, The order of the rotational symmetry is $3$ since we get the original shape of equilateral triangle $3$times.
For Regular Hexagon: -
Rotate a regular hexagon $60{}^\circ $ then we have
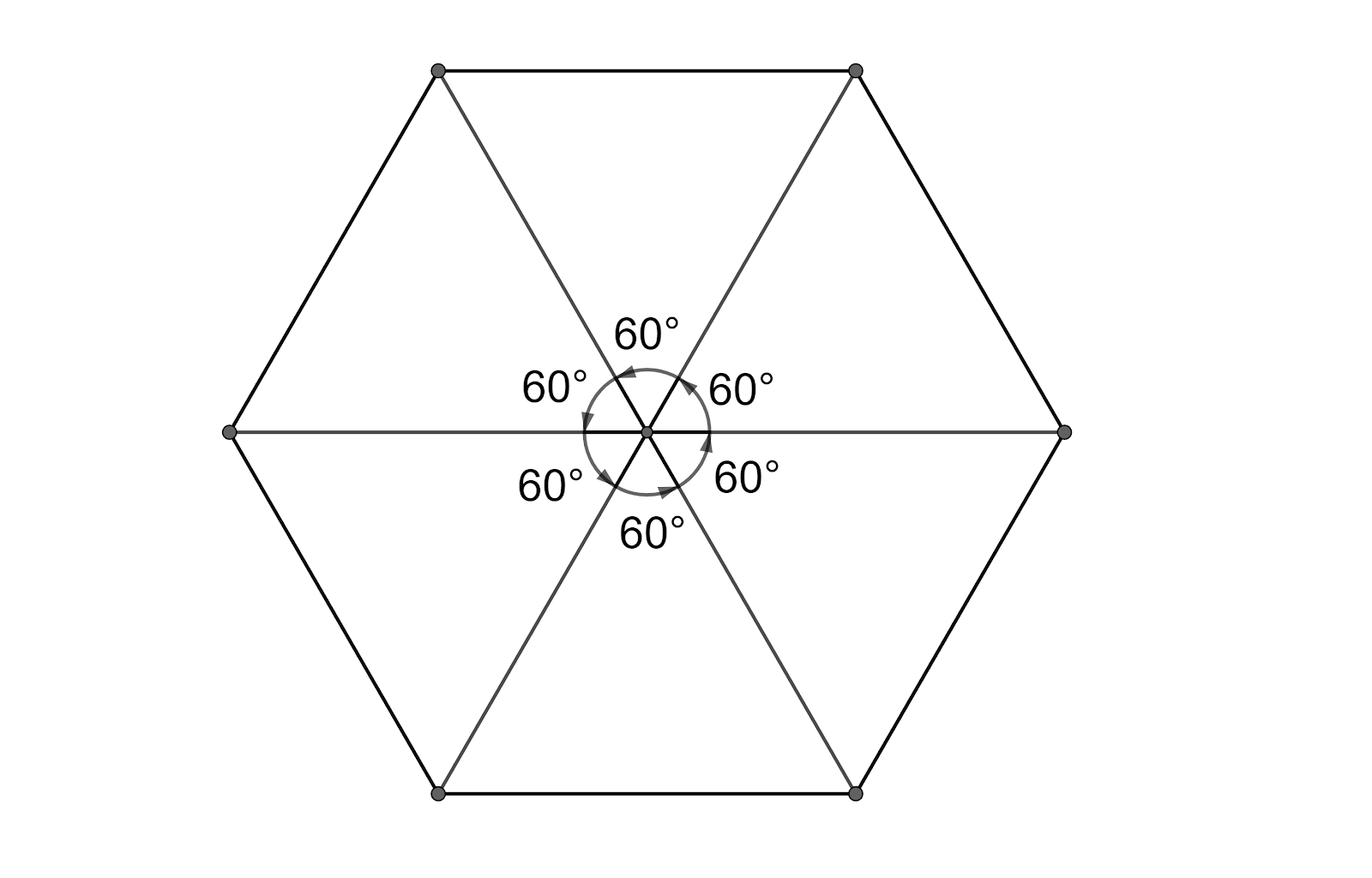
Here we have intersection point of diagonals as Centre of the Rotation, the angle of rotation is $60{}^\circ $ since we have the original shape of regular hexagon when it is rotated $60{}^\circ $, The order of the rotational symmetry is $6$ since we get the original shape of regular hexagon$6$ times.
For Circle: -
A sample circle is shown below
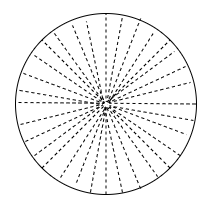
We have the center of the circle as the center of the rotation and the order of the rotation is infinite since we get the exact shape of the circle if we rotate it with $1{}^\circ $, so the order of the rotation is undefined.
For Semi-Circle: -
A sample semi-circle is given below

We have the center of the semi-circle as the center of the rotation and the rotation angle is $360{}^\circ $ since we get the exact shape of the semi-circle when it is rotated $360{}^\circ $ and the order of the rotation symmetry is $1$.
Hence
Note: Before going to this problem we need to know some basic concept that is ‘Rotational Symmetry’.
The Rotational Symmetry of a shape explains that when an object is rotated on its own axis, the shape of the object looks the same.
Center of Rotation for an object that has rotational symmetry, is the fixed point around which the rotation occurs is called the center of rotation.
Order of Rotational symmetry for an object that has rotational symmetry, is the number of positions in which a figure can be rotated and still appears exactly as it did before the rotation.
Angle of Rotational Symmetry for an object that has rotational symmetry, is the angle of turning during rotation is called the angle of rotation.
Complete step-by-step answer:
For Square: -
We will consider a square and take the position of a vertex $p$ of the square in order to distinguish the position of the square. We are going to rotate the square $90{}^\circ $ as shown in below





Here we have Intersection point of diagonals as Centre of the Rotation, the angle of rotation is $90{}^\circ $, The order of the rotational symmetry is $4$.
For Rectangle: -
We will consider a rectangle and we will rotate the rectangle $90{}^\circ $ as shown in figure.





Here we have intersection point of the diagonals as Centre of the Rotation, the angle of rotation is $180{}^\circ $ since we have the original shape of rectangle when it is rotated $180{}^\circ $, The order of the rotational symmetry is $2$ since we get the original shape of rectangle $2$times.
For Rhombus: -
Rotate the rhombus $90{}^\circ $ then we have,





Here we have intersection point of the diagonals as Centre of the Rotation, the angle of rotation is $180{}^\circ $ since we have the original shape of rhombus when it is rotated $180{}^\circ $, The order of the rotational symmetry is $2$ since we get the original shape of rhombus $2$times.
For Equilateral Triangle: -
Take an equilateral triangle and rotate it $120{}^\circ $, then we have




Here we have intersection point of medians as Centre of the Rotation, the angle of rotation is $120{}^\circ $ since we have the original shape of equilateral triangle when it is rotated $120{}^\circ $, The order of the rotational symmetry is $3$ since we get the original shape of equilateral triangle $3$times.
For Regular Hexagon: -
Rotate a regular hexagon $60{}^\circ $ then we have

Here we have intersection point of diagonals as Centre of the Rotation, the angle of rotation is $60{}^\circ $ since we have the original shape of regular hexagon when it is rotated $60{}^\circ $, The order of the rotational symmetry is $6$ since we get the original shape of regular hexagon$6$ times.
For Circle: -
A sample circle is shown below

We have the center of the circle as the center of the rotation and the order of the rotation is infinite since we get the exact shape of the circle if we rotate it with $1{}^\circ $, so the order of the rotation is undefined.
For Semi-Circle: -
A sample semi-circle is given below

We have the center of the semi-circle as the center of the rotation and the rotation angle is $360{}^\circ $ since we get the exact shape of the semi-circle when it is rotated $360{}^\circ $ and the order of the rotation symmetry is $1$.
Hence
| Figure | Center of rotational | Order of rotational | Angle of rotational |
| Square | Intersection Point of Diagonals | $4$ | $90{}^\circ $ |
| Rectangle | Intersection Point of Diagonals | $2$ | $180{}^\circ $ |
| Rhombus | Intersection Point of Diagonals | $2$ | $180{}^\circ $ |
| Equilateral triangle | Intersection Point of Medians | $3$ | $120{}^\circ $ |
| Regular hexagon | Intersection Point of Diagonals | $6$ | $60{}^\circ $ |
| Circle | Center | Infinite | At every Point |
| Semi-circle | Center or Midpoint of diameter | $1$ | $360{}^\circ $ |
Note: Before going to this problem we need to know some basic concept that is ‘Rotational Symmetry’.
The Rotational Symmetry of a shape explains that when an object is rotated on its own axis, the shape of the object looks the same.
Center of Rotation for an object that has rotational symmetry, is the fixed point around which the rotation occurs is called the center of rotation.
Order of Rotational symmetry for an object that has rotational symmetry, is the number of positions in which a figure can be rotated and still appears exactly as it did before the rotation.
Angle of Rotational Symmetry for an object that has rotational symmetry, is the angle of turning during rotation is called the angle of rotation.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

What is pollution? How many types of pollution? Define it




