Question

Fill in the blanks with similar/not similar
(iii) All isosceles triangles are __________.

Answer 1

Hint: Isosceles triangles are those which have two equal sides. Two triangles are similar if and only if their corresponding sides are proportional.


Complete step by step solution:
Now, in this question we need to find out whether isosceles triangles are similar or not.
To find out , let us consider two isosceles triangles $\Delta ABC$ and $\Delta DEF$ , such that in $\Delta ABC$, $AB = AC$ and in $\Delta DEF$, $DE = DF$ .

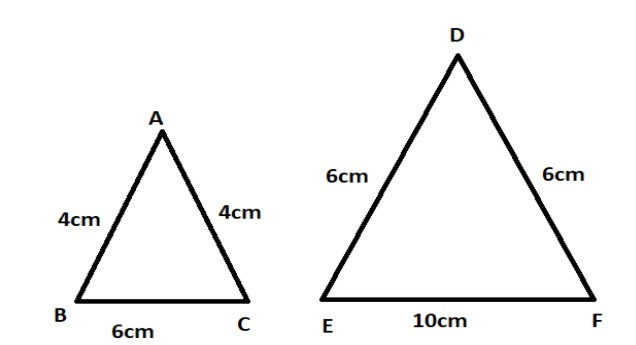
$\Delta ABC$ is such that $AB = AC = 4cm$and $BC = 5cm$ while in $\Delta DEF$ we have $DE = DF = 6cm$ and $EF = 10cm$ .
Now for two triangles to be similar their ratios should be proportional.
So for $\Delta ABC$ to be similar to $\Delta DEF$, their ratios must be proportional.
That is, we need to prove :
$\dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}} = \dfrac{{BC}}{{EF}}$
So, putting $AB = AC = 4cm$, $BC = 5cm$and $DE = DF = 6cm$, $EF = 10cm$ we will get:
$\dfrac{{AB}}{{DE}} = \dfrac{4}{6} = \dfrac{2}{3}$
$\dfrac{{AC}}{{DF}} = \dfrac{4}{6} = \dfrac{2}{3}$
and $\dfrac{{BC}}{{EF}} = \dfrac{6}{{10}} = \dfrac{3}{5}$$\dfrac{{AB}}{{DE}}$
so, clearly, $\dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}} = \dfrac{4}{6} = \dfrac{2}{3}$ which is not proportional to the ratio of the third sides since the ratio of third sides is $\dfrac{{BC}}{{EF}} = \dfrac{6}{{10}} = \dfrac{3}{5}$.
Hence, although the two triangles $\Delta ABC$ and $\Delta DEF$ are isosceles but they are not similar since not all of their corresponding sides are proportional. One two of the corresponding sides are proportional while the third side is not.
Therefore $\Delta ABC$ and $\Delta DEF$ are not similar.
Therefore,
All isosceles triangles are not similar.

Note: Apart from the corresponding sides being proportional, there is a perimeter and area property also for similar triangles which can also be used to prove that the two isosceles triangles are not always similar