Question

How do you find a feasible region using linear programming?

Answer 1

Hint: These types of solutions are pretty straight forward and are very easy to solve if we follow all the steps perfectly. According to the theory of Linear Programming Problems, we have to remember that a BFS or basic feasible solution is one, which has the minimum set of non-zero parameters. For a given problem, if we plot its graph, then we get a polyhedron, and each corner of this formed polyhedron represents a very simple feasible solution.

Complete step by step answer:
Now we start off the solution by saying that, in case of a Linear Programming Problem, we are given an objective function and we need to maximize or minimize the objective function under some constraints. The solution that we get on solving, keeping in mind of all the constraints, is known as a feasible solution.
Let us assume that we have an objective function, \[z=4x+3y\] and we need to maximize this objective function under some constraints. The constraints are,
\[\begin{align}
  & x+2y\le 7, \\
 & 2x+y\ge 1, \\
 & -3x+y\le 2 \\
\end{align}\]
Here we have \[x\ge 0\] and \[y\ge 0\] as the non-negative restrictions.
Now, first of all we plot all the given constraints in a graph paper. After plotting, we need to mark all the regions which satisfy the constraints with respect to the origin.

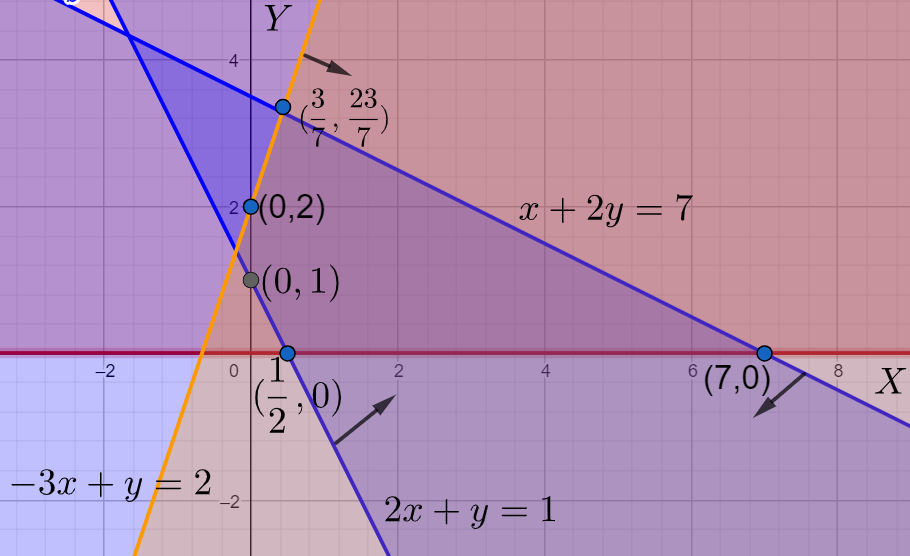
From the graph we can very easily see that, there are five points of the polyhedron so formed which form the feasible solution. From these five points, one of them will be the actual solution. We now put all the five solutions in the objective functions and check for which point the objective function has maximum value. We see that the objective function has maximum value for \[x=7\] and \[y=0\] . Thus this forms the actual solution of our LPP.


So, the correct answer is “Option C”.

Note: In case of these types of LPP problems, we first need to form the objective function from the problem description. After this we need to plot all the constraints in a graph paper and find out all the feasible solutions. After finding out the feasible solutions, we need to put them one by one on the objective function to check which of them gives the maximum or minimum value as given in the problem.