Question

Find acceleration of centre of mass of the system as shown:

Answer 1

Hint: Centre of the mass of the body is the point on which the whole mass is assumed to be concentrated. The concept of centre of mass is very important in solving mechanics problems. We can easily predict the trajectory of the motion of complex bodies. If the net force on the body is zero, then the center of mass of the body will not change its velocity, but it may be possible that some part of the body is undergoing complex rotational motion.

Formula used:
$\sum F_{net} = m_T a_{com}$

Complete answer:
The acceleration of centre of mass could be easily calculated using $\sum F_{net} = m_T a_{com}$, where $F_{net}$ is the net external force on the system and $m_T$ is the total mass of the system.

The net external force on the block of 2kg $= -10N + f$
$\implies -10 + \mu\times mg$
$\implies -10+0.1 \times 20 =-10+ 2$
$= -8N$

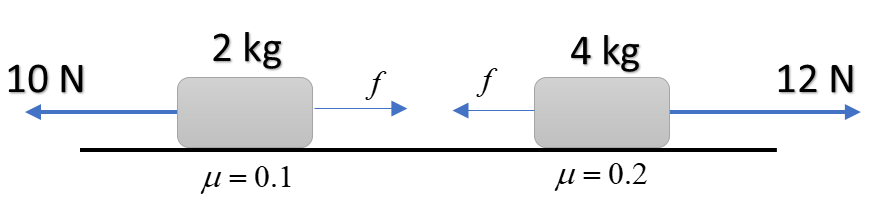
The net external force on the block of 10kg $= 12N - f$
$\implies 12 - \mu\times mg$
$\implies 12-0.2 \times 40 =12- 8$
$= 4N$

Now, the net external force on the system is $-8+4 = -4N$
Also, the total mass of the system is 2 kg + 4 kg = 6kg
Hence, $F_{net} = m_T a_{com}$
Thus $a_{com} = \dfrac{-4}{6} = -2/3ms^{-2}$
Hence the net acceleration of the centre of mass of the system is $-2/3\ ms^{-2}$.

Note:
Always note that the frictional force on a body is applied opposite to the direction of motion of the body. Here, one body is moving towards the left. Thus the direction of the force of friction is taken towards the right and the other is moving right, hence direction is taken towards left. In the final expression, acceleration is $-2/3\ ms^{-2}$. The negative sign shows that the acceleration is towards the left or the whole system’s centre of mass is accelerating towards the left.