Question

Find all possible lengths of the third side of a triangle, if sides of the triangle are 3 and 9.
(a) $6 < x < 12$
(b) $5 < x < 12$
(c) $6 < x < 10$
(d) $6 < x < 11$

Answer 1

Hint: We know the property of a triangle that the sum of the two sides is greater than the third side. So, let us assume the third side be x so using the above property three inequalities could be possible $x+3>9$, $x+9>3$, $3+9>x$.Now, find the intersection of all these three inequalities.

Complete step by step answer:
Two sides of the triangle given in the question are:
3 & 9
Let us assume that the third side is “x”.
We have to find the possible lengths of the third side which we can find using the property that the sum of two sides is greater than the third side.
$x+3>9$
$x+9>3$
$3+9>x$
Solving the first inequality we have,
$\begin{align}
  & x+3>9 \\
 & \Rightarrow x>6 \\
\end{align}$
Solving the second inequality we have,
$\begin{align}
  & x+9>3 \\
 & \Rightarrow x>-6 \\
\end{align}$
Solving the third inequality we have,
$3+9>x$
$\Rightarrow 12>x$
Now, finding the intersection of $x>6,x>-6,x<12$ we get,
$6From the above solution, we have got the possible lengths of the third side of the triangle as $6Hence, the correct option is (a).

Note: You might wonder how we have found the intersection of the three inequalities in the above solution which we are shown below.
The three inequalities that we have got above are:
$x>6,x>-6,x<12$
On the number line, we have drawn the inequalities like $x>6$ is denoted by B, $x>-6$ is denoted by A and $x<12$ is denoted by C.

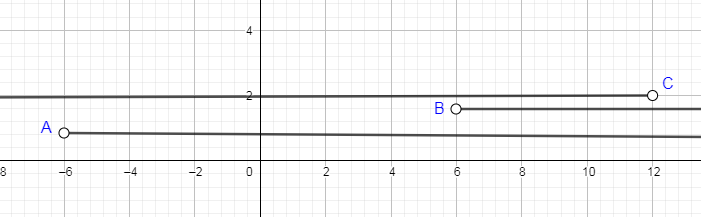
From the above drawing, you can see that the overlapping region of the three inequalities is from B to C which we can write in mathematical terms as $6In the above drawing, you can also see that point A, B and C is denoted by empty dot. The empty dot means that the number on which that dot is not included like x is greater than -6 not greater than or equal to -6.