
How do you find all solutions between 0 to
Answer
469.8k+ views
Hint: In the equation
Complete step by step answer:
The given equation in the question is
First let’s find the value of sin x that satisfy the equation
Let’s add 3 in both LHS and RHS , by adding 3 both sides we get
Diving LHS and RHS by 4 we get
So the value of sin x is
So we have find the value of x for which sin x is equal to
Let’s solve this by graph
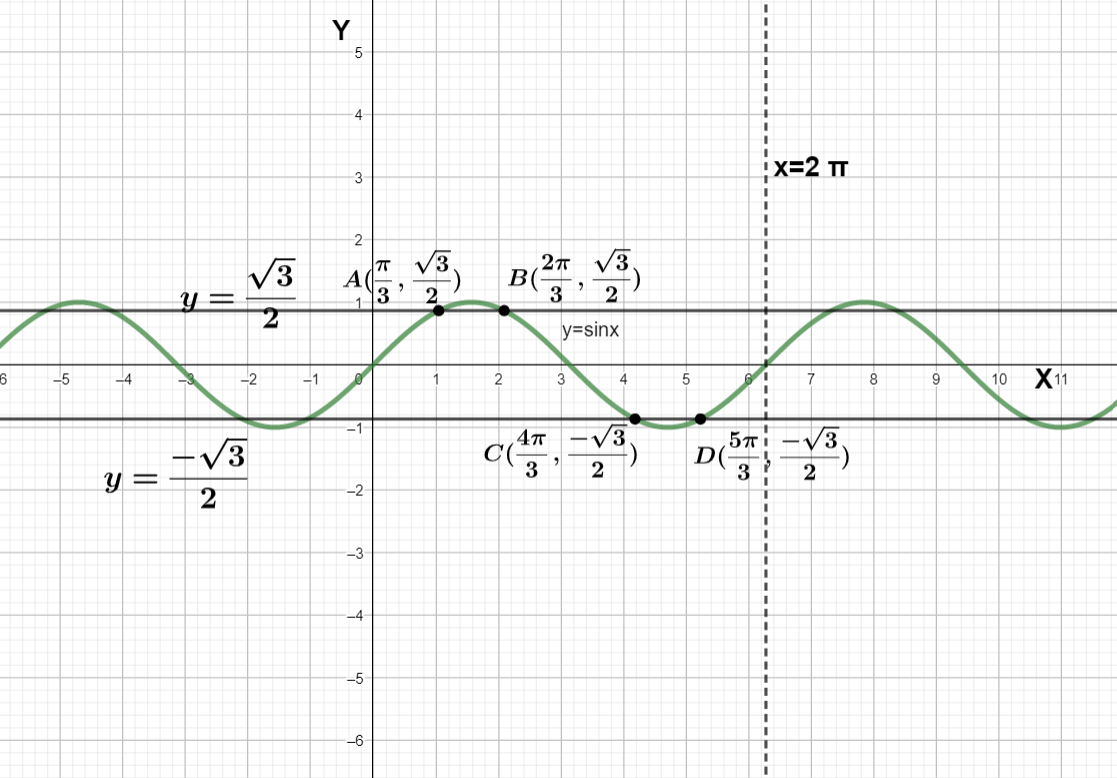
We can see the point of intersection the 2 line with y= sin x are A , B, C, and D
So all the solutions from 0 to
Note:
We can check all the solutions whether these are correct or not by putting the value of x in the equation. When we put
Complete step by step answer:
The given equation in the question is
First let’s find the value of sin x that satisfy the equation
Let’s add 3 in both LHS and RHS , by adding 3 both sides we get
Diving LHS and RHS by 4 we get
So the value of sin x is
So we have find the value of x for which sin x is equal to
Let’s solve this by graph

We can see the point of intersection the 2 line with y= sin x are A , B, C, and D
So all the solutions from 0 to
Note:
We can check all the solutions whether these are correct or not by putting the value of x in the equation. When we put
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




