Question

How do you find an area of a triangle?

Answer 1

Hint: For finding the area of a triangle or proving the area of a triangle we need to understand the rectangle always when we want to calculate the area of the triangle or proving it then we need the right-angle triangle in which we have height and the base. So, if we want to prove an area of a triangle then we need a rectangle so that we can prove it.

Complete step by step Solution:
Given that –
We need to find the area of a triangle.
Prove that –
Prove the area of a triangle is the $\dfrac{1}{2} \times base \times height$.
Prove –
We know that
The area of triangle $ = $ the area of right-angle triangle $ = $ $\dfrac{1}{2}$$[$area of an rectangle$]$
Let – a rectangle $ABCD$ in which we have diagonal $AC$ then

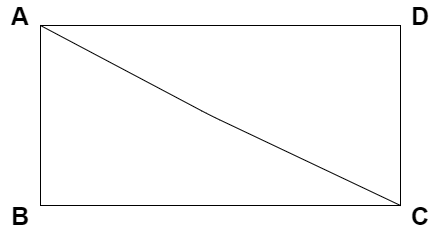
Now we know that the area of a rectangle is the $(length \times breadth)$
Now we can see in the diagram that our rectangle $ABCD$ is divided into two parts by the diagonal $AC$ so in our rectangle $ABCD$ in which we have $length = AB$ and $breadth = BC$.
Now we will put these values in our rectangle area formula $(length \times breadth)$ then
Now we will get the area of a rectangle which is $(AB \times BC)$
Now for finding the area of our right-angle triangle is the $\dfrac{1}{2}$$[$area of a rectangle$]$
Now the area of a triangle is the $\dfrac{1}{2}(AB \times BC)$

Therefore, the area of a triangle is the $\dfrac{1}{2}(AB \times BC)$.

Note: Always remember that if we want to find the area of any triangle then we need a right-angle triangle because for finding the area of a triangle we need two things one is the height of the triangle and another is the base of our triangle.