
How do you find an asymptote of quadratic equations?
Answer
462.9k+ views
Hint: Now to check if the asymptotes of the function we will first check the value of function at which the function is not defined. Then we will check the end behavior of the function to find horizontal asymptote. Hence we will find the asymptote of the equation.
Complete step by step solution:
Now let us first understand the concept of asymptotes.
Asymptotes are lines which represent a value which a curve approaches but never reaches.
Now let us first understand two main types of asymptotes.
Horizontal asymptotes are lines which are parallel to the x axis and the curve tends to reach the value represented by the line but never reaches.
Now let us say as
Hence y = b is the horizontal asymptote of the curve.
Now similarly consider vertical asymptote.
Horizontal asymptotes are lines which are parallel to y axis and the curve tends to reach the value represented by the line but never reaches.
This case occurs when the function is not defined on some value x.
Now a function is not defined for the values where denominator is 0,
Hence we get a horizontal asymptote in this case.
Check the graph to understand.
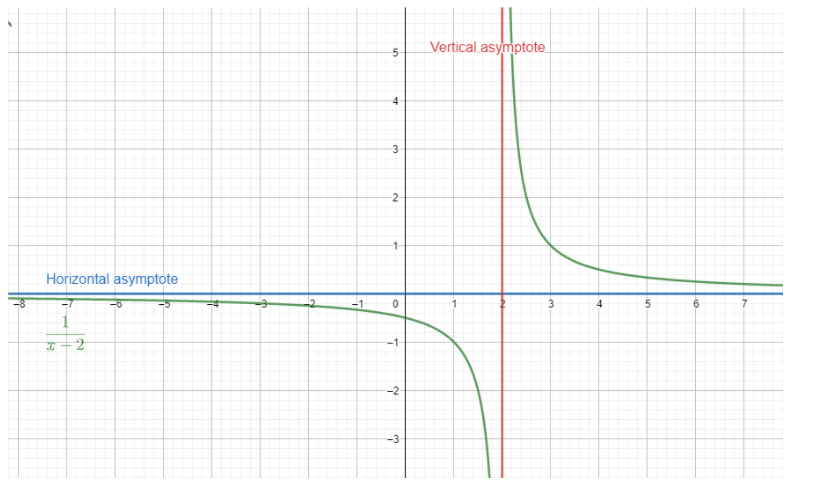
For example consider the example
Now consider the quadratic equation
Now the quadratic function is a polynomial and hence is defined on all values of x.
Hence we do not have vertical asymptote for the curve.
Now similarly as
Hence the curve reaches all the points.
Hence the function has no horizontal asymptote.
Hence the quadratic equation has no asymptote.
Note: Now if we have a function of the form
Complete step by step solution:
Now let us first understand the concept of asymptotes.
Asymptotes are lines which represent a value which a curve approaches but never reaches.
Now let us first understand two main types of asymptotes.
Horizontal asymptotes are lines which are parallel to the x axis and the curve tends to reach the value represented by the line but never reaches.
Now let us say as
Hence y = b is the horizontal asymptote of the curve.
Now similarly consider vertical asymptote.
Horizontal asymptotes are lines which are parallel to y axis and the curve tends to reach the value represented by the line but never reaches.
This case occurs when the function is not defined on some value x.
Now a function is not defined for the values where denominator is 0,
Hence we get a horizontal asymptote in this case.
Check the graph to understand.

For example consider the example
Now consider the quadratic equation
Now the quadratic function is a polynomial and hence is defined on all values of x.
Hence we do not have vertical asymptote for the curve.
Now similarly as
Hence the curve reaches all the points.
Hence the function has no horizontal asymptote.
Hence the quadratic equation has no asymptote.
Note: Now if we have a function of the form
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




