
Find and draw a transverse common tangent to two circles of radii 6cm and 2cm whose centres are 8cm apart.
Answer
525.3k+ views
Hint: Derive the length of a transverse tangent in terms of radii of both the circle and the distance between their centres. Radii joining the transverse tangent will be parallel to each other. And use the concept that if the sum of radii of both the circles is equal to distance between centres then they will touch each other.
Complete step-by-step answer:
Let us derive the relation to get the length common transverse tangent for two circles. So, length of transverse tangent can be calculated as
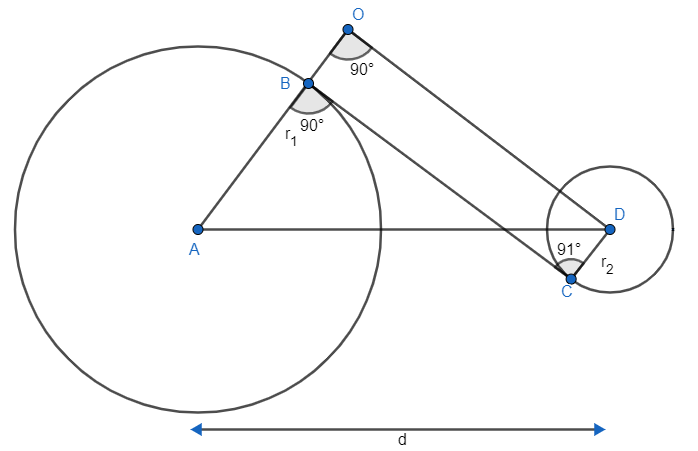
Now, as we know radius and tangent are perpendicular to each other at the point of tangency and we also know there is only one perpendicular direction for any line i.e. direction of perpendicular to any line will be unique.
As,
From the diagram and two of the angles of quadrilateral
Hence, ODCB will be a rectangle with equal opposite sides and all the angles of it will be
Now, we know
In triangle OAD we can apply Pythagoras theorem as
As, OBCD is a rectangle, so, OD = BC. Hence, we can write above equation as
Transverse common tangent length as
Now, coming to the question we are given two circles of radii 6cm and 2cm and distance between their centres is 8cm. So, we can apply the above mentioned result to get the length of the transverse common tangent. So, we get
Where d is distance between centres and
Hence, we get length of transverse common tangent as
Hence, no transverse tangent will touch each circle at one point where circles will touch each other as well. It can be observed by the relation among radii and distance between centres. We get,
So, distance between centres is equal to the sum of their radii. It means both the circles will touch each other.
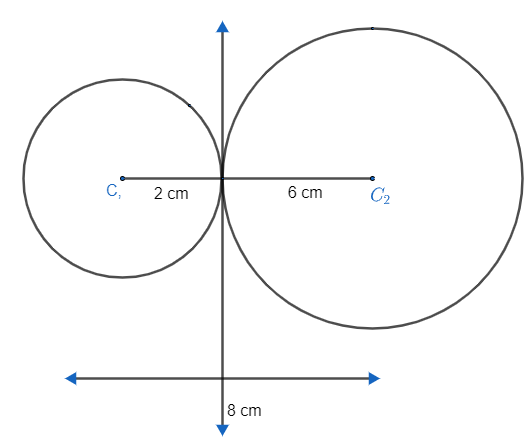
Note: We don’t need to derive a formula for length of transverse common tangent for the given circles as they are touching each other, so we can directly give the length as 0, but for the future reference and other problems of the same type, where circles will not meet. So, be clear with the formula as well.
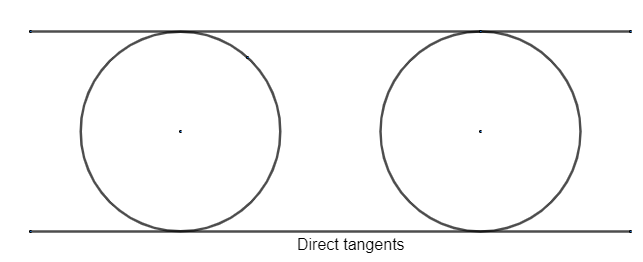
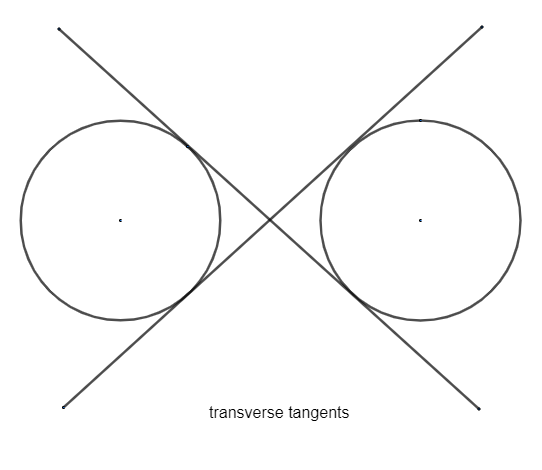
Be clear with the transverse and direct common tangents. Both can be drawn as
Complete step-by-step answer:
Let us derive the relation to get the length common transverse tangent for two circles. So, length of transverse tangent can be calculated as

Now, as we know radius and tangent are perpendicular to each other at the point of tangency and we also know there is only one perpendicular direction for any line i.e. direction of perpendicular to any line will be unique.
As,
From the diagram and two of the angles of quadrilateral
Hence, ODCB will be a rectangle with equal opposite sides and all the angles of it will be
Now, we know
In triangle OAD we can apply Pythagoras theorem as
As, OBCD is a rectangle, so, OD = BC. Hence, we can write above equation as
Transverse common tangent length as
Now, coming to the question we are given two circles of radii 6cm and 2cm and distance between their centres is 8cm. So, we can apply the above mentioned result to get the length of the transverse common tangent. So, we get
Where d is distance between centres and
Hence, we get length of transverse common tangent as
Hence, no transverse tangent will touch each circle at one point where circles will touch each other as well. It can be observed by the relation among radii and distance between centres. We get,
So, distance between centres is equal to the sum of their radii. It means both the circles will touch each other.

Note: We don’t need to derive a formula for length of transverse common tangent for the given circles as they are touching each other, so we can directly give the length as 0, but for the future reference and other problems of the same type, where circles will not meet. So, be clear with the formula as well.
Be clear with the transverse and direct common tangents. Both can be drawn as


Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




