Question

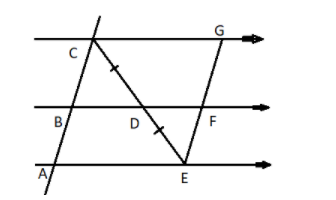
Find DF, if CG = 11cm

$\left( a \right)$ 5.6 cm
$\left( b \right)$ 5.5 cm
$\left( c \right)$ 0.55 cm
$\left( d \right)$ 55 cm

Answer 1

Hint: In this particular question use the concept that if we prove that the triangles CEG and DEF are similar to each other then we easily calculate the length of DF, by using property of similar triangles so use these concepts to reach the solution of the question.

Complete step-by-step answer:
It is given that in the given figure CG = 11 cm
Now we have to find out the length of DF.
From the figure we can say that CG, BF and AE are parallel w.r.t each other.
And CA parallel to GE.
And from figure CD = DE
Therefore, CE = CD + DE = DE + DE = 2DE
So, CE = 2DE................... (1)
Now in triangle CEG and triangle DEF we have,
$\angle CEG = \angle DEF$ (Common angle)
$\angle CGE = \angle DFE$ (Corresponding angles since CG parallel to BF, so CG||DF)
$\angle GCE = \angle FDE$ (Corresponding angles since CG parallel to BF, so CG||DF)
Therefore, by AAA congruence triangle CEG is similar to triangle DEF.
I.e. both the triangles are concurrent.
$ \Rightarrow \Delta CEG \sim \Delta DEF$
Now as we know that in similar triangles the ratio of the corresponding sides are equal.
Therefore, $\dfrac{{CG}}{{DF}} = \dfrac{{CE}}{{DE}} = \dfrac{{GE}}{{FE}}$
$ \Rightarrow \dfrac{{CG}}{{DF}} = \dfrac{{CE}}{{DE}}$
Now from equation (1) we have,
$ \Rightarrow \dfrac{{CG}}{{DF}} = \dfrac{{2DE}}{{DE}} = 2$
Now substitute the value of CG we have,
$ \Rightarrow \dfrac{{11}}{{DF}} = 2$
$ \Rightarrow DF = \dfrac{{11}}{2} = 5.5$ cm
So this is the required answer.
Hence option (b) is the correct answer.

Note:Whenever we face such types of questions the key concept we have to remember is that when two triangle are similar the ratio of the corresponding sides are equal, and also remember that a line cut two parallel lines so the angle made by the line (i.e. corresponding angles) are equal, so simply substitute the values in this equation of ratios as above and simplify we will get the required answer.