Question

Find magnitude of force exerted by string on the pulley.

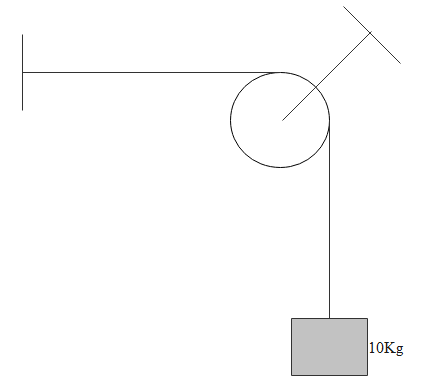
A. $100{\text{ N}}$
B. $100\sqrt 2 {\text{ N}}$
C. $200{\text{ N}}$
D. $\sqrt {100} {\text{ N}}$

Answer 1

Hint: When a block is connected to the string and when it was given that the system is in equilibrium then here must be some force that balances the weight of the block and that force will be the tension and that will be equal to weight and tension is always a pulling force.
Formula used:
$\eqalign{
  & {\text{T = mg}} \cr
  & \cr} $

Complete answer:
The string used here is the same i.e the vertical portion of the string which connects the block and pulley and the horizontal portion of the string which connects the support and the pulley is the same. As long as the string is the same and massless the tension will be the same for both the portions. Since the system is in equilibrium the weight of the block is compensated by the tension in the string. So the weight of the block is a product of mass and acceleration due to gravity. Let the weight be W and mass be ‘m’ and acceleration due to gravity be ‘g’.

So the weight will be
${\text{W = mg}}$
Mass is given as 10Kg and acceleration due to gravity is $10kg/{m^2}$
${\text{W = mg}}$
$\eqalign{
  & \Rightarrow W{\text{ }} = {\text{ }}10 \times 10 \cr
  & \Rightarrow W{\text{ }} = {\text{ }}100N \cr} $
And the tension is ‘T’ is equal to the weight.
$\eqalign{
  & {\text{T = mg}} \cr
  & \cr} $
$\eqalign{
  & \Rightarrow {\text{T = 100N}} \cr
  & \cr} $

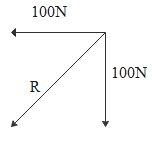
Since the angle between the two tensions is ninety degrees. The resultant will be
$\sqrt {{{100}^2} + {{100}^2}} = 100\sqrt 2 $

So, the correct answer is “Option B”.

Note:
The resultant of the tension forces will be the force acting on the pulley. That force will pass through the center of the pulley hence the torque produced by that force about the pulley center will be zero. Even though if we take the torques produced by the two forces individually the net torque will be zero.