Question

Find out the quadrant of the point which divides internally the line segment joining (3, 4) and (7,-6) in two parts where one part is twice longer than the other.\[\]
(a)\[\text{I}\]
(b) \[\text{II}\]
(c) \[\text{III}\]
(d) \[\text{IV}\]

Answer 1

Hint: A point can divide the line segment either internally or externally. If the point is on the line segment then the point divides the line segment internally at any particular ratio. The line is going to cut the line segment only internally, we only need to take care of the internal case using the section formula.

Complete step-by-step solution:
We know from section formula that if any point $P(x,y)$ which divides a line segment internally $\overline{AB}$ in a ratio $AP:PB=m:n$ with endpoints $A({{x}_{1}},{{y}_{2}})\text{ and B(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{)}$ then the coordinates of P are given by
\[\begin{align}
  & x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n} \\
 & y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \\
\end{align}\]

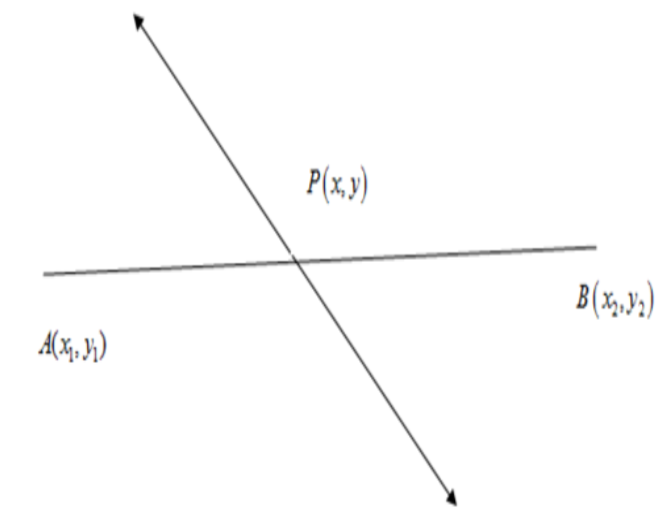
Let us assume that the line divides the line segment internally at the point $P$. Here the coordinates of endpoints $A$ and $B$ are given as $\left( 3,4 \right)$ and (7,-6). According to the question, $P$ can divide the line segment $\overline{AB}$ such that one part is twice the other. We can see it raises two cases.
Case 1:
 If the line divides in ratio $2:1$ or AP is twice PB, then $m:n=2:1$. Then the co-ordinates of P are
\[\begin{align}
  & x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}=\dfrac{2(7)+1(3)}{2+1}=\dfrac{17}{3} \\
 & y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}=\dfrac{2(-6)+1(4)}{2+1}=-\dfrac{8}{3} \\
\end{align}\]
As $x$ is positive and $y$ is negative, P lies in fourth(IV) quadrant. \[\]

Case 2:
If the line divides in ratio 1:2 or PB is twice AP , then $m:n=1:2$. Hence the co-ordinates of P are
\[\begin{align}
  & x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}=\dfrac{1(7)+2(3)}{2+1}=\dfrac{13}{3} \\
 & y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}=\dfrac{1(-6)+2(4)}{2+1}=\dfrac{2}{3} \\
\end{align}\]
As both $x\text{ and }y$ are positive, P lies in first (I) quadrant. The correct choices are A(I) and D(IV).

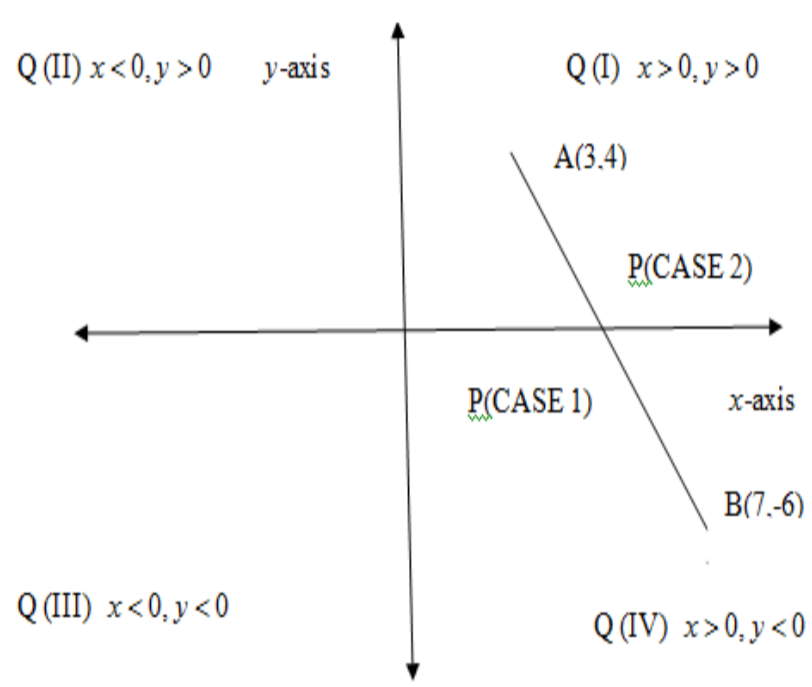
We can observe from the above image the two possible positions in two different quadrants of P in the $xy-$ plane.

Note: We need to be careful to choose sectional formula from the confusion of internal and external division of a line segment. As the question is ambiguous about the ratio of division, it makes two cases. It more than one option correct type of MCQ.