Question

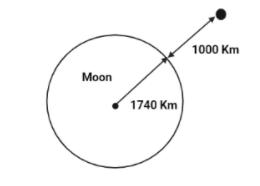
Find the acceleration due to gravity of the moon at a point 1000 km above the moon's surface. The mass of the moon is $7.4 \times {10^2}Kg$ and its radius is $1740Km$.

Answer 1

Hint: For the above question we will equate the gravitational force between the moon and the body to the force exerted on the body.

Complete step by step solution:
We know that there will be a gravitational force exerted between the body and the moon, which is represented by the following formula:
$F = \dfrac{{GMm}}{{{{(r + h)}^2}}}$
Where $G$ is the gravitational force,
$M$ is the mass of the moon,
$m$ is the mass of the body,
$r$ is the radius of the moon and
$h$ is the distance between the moon surface and the body

The force exerted on the body is $F = ma$ where $a$ is the acceleration.
Now, this force is equal to the gravitational force. Hence,
$
  \dfrac{{GM{m}}}{{{{(r + h)}^2}}} = {m}a \\
  \dfrac{{GM}}{{{{(r + h)}^2}}} = a \\
 $
Substituting the values we will get,
$
  a = \dfrac{{6.67 \times {{10}^{ - 11}} \times 7.14 \times {{10}^{22}}}}{{{{(1740 + 1000)}^2} \times {{10}^6}}} \\
  a = \dfrac{{49.358 \times {{10}^{11}}}}{{0.75 \times {{10}^{13}}}} \\
\Rightarrow a = 65.8 \times {10^{ - 2}} \\
\Rightarrow a = 0.65m.{\sec ^{ - 2}} \\
 $
Therefore, the acceleration due to gravity of the moon at a point 1000 km above the moon's surface is $0.65m.{\sec ^{ - 2}}$.

Note:
The total gravity on the surface of the Earth is $9.8m.{\sec ^{ - 1}}$. When an object is thrown from a building's roof or a cliff's apex, for example, it travels toward the earth. The gravity on the Moon's surface is about $\dfrac{1}{6}th$ as strong, or about $1.6m.{\sec ^{ - 1}}$.