Question

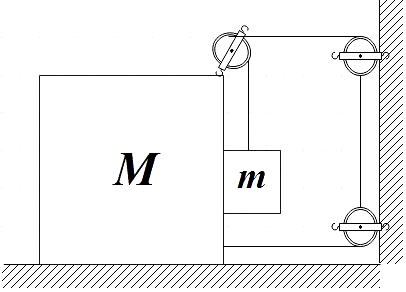
Find the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is ${\mu }_1$ and that between the bigger block and the ground is ${\mu }_2$.

Answer 1

Hint: For the problems involving mass-pulley system, first we have to find all the accelerations acting on each of the given bodies. Then we have to draw the free body diagrams for each mass separately. Now by balancing the forces in both vertical and horizontal directions and then doing the necessary substitutions accordingly gives you the required acceleration.

Complete answer:
Let us assume that the body of mass M is accelerated towards the right with acceleration$a$and we are asked to determine this acceleration. The mass m attached to mass M will also have an acceleration of ‘a’ towards right and also, due to string constraint motion of the given system, the mass m also has an acceleration 2a in the downward direction.
Now that we have determined all the accelerations on the given masses, let us make free-body diagrams for each of the masses. The free-body diagram of mass m is given by,

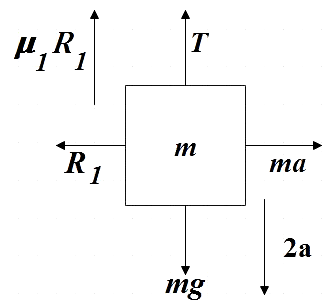
We see that the forces acting on mass m are: frictional force between two surfaces, weight downward, tension upward, normal reaction towards left, force due acceleration towards right and force due acceleration 2a downward. Now by balancing the forces in the vertical direction, we get,
$mg-T-{\mu }_{1}R=m\left(2a\right)$
But, $R=ma$
$\Rightarrow T=mg-2ma-{\mu }_{1}ma$ …………………………… (1)

Free body diagram of mass M:

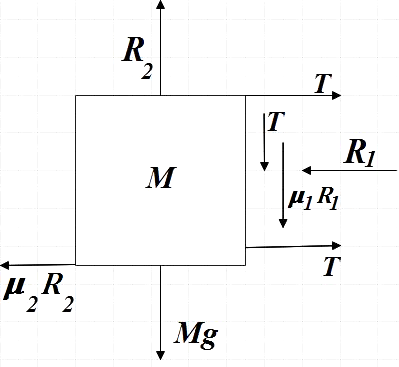
Balancing the vertical forces on M, we get,
$R_2=Mg+{\mu }_{1}ma+T$ ……………………………. (2)
Balancing the horizontal forces on M gives,
$2T-R_1-{\mu }_2{R}_2=Ma$
Substituting (2),
$2T-ma-{\mu }_2(Mg+{\mu }_{1}ma+T)=Ma$
Substituting (1),
$2(mg-2ma-{\mu }_{1}ma)-ma-{\mu }_2(Mg+{\mu }_{1}ma+mg-2ma-{\mu }_{1}ma)=Ma$
$\Rightarrow 2mg-5ma-2{\mu }_{1}ma+2{\mu }_{2}ma-{\mu }_{2}Mg-{\mu }_{2}mg=Ma$
$\Rightarrow Ma+5ma+2{\mu }_{1}ma-2{\mu }_{2}ma=2mg-{\mu }_{2}Mg-{\mu }_{2}mg$
$\Rightarrow a(M+m(5+2({\mu }_1-{\mu }_2)))=g(2m-{\mu }_2(M+m))$
$\Rightarrow a={\displaystyle \frac{(2m-{\mu }_2(M+m))g}{(M+m(5+2({\mu }_1-{\mu }_2)))}}$
Hence we get the acceleration of the block of mass M as,
$a={\displaystyle \frac{(2m-{\mu }_2(M+m))g}{(M+m(5+2({\mu }_1-{\mu }_2)))}}$

Note:
While drawing the free body diagrams, make sure that you don’t miss any of the forces acting on the masses. While marking the accelerations on the bodies keep in mind that you are dealing with a string constraint system. Also, chances are that you may miss normal forces while substituting, so take care of that too.