
Find the additive and multiplicative inverse of $ - \;\dfrac{8}{3}$
Answer
541.8k+ views
Hint:We have to find additive and multiplicative inverse of the given number. We know that two numbers are additive inverses if their sum is equals to zero whereas; two numbers are multiplicative inverses when their product is equals to one. Using the definitions we solve the problem.
Complete solution step by step:
Firstly we write down the number of which we want to find the additive and multiplicative inverses i.e.
$ - \;\dfrac{8}{3}$
We will find the additive inverse first using its definition i.e. two numbers are additive inverses if the sum of two is equals to zero. So we let a number to be $a$ and translating the definition into mathematical expression we have -
$ - \dfrac{8}{3} + a = 0$
Now we simply have to solve this algebraic equation to find the additive inverse so we transfer the constant part to the RHS of the equation to get -
$ \Rightarrow a = \dfrac{8}{3}$
This is the additive inverse of the given number.
Now we try to find the multiplicative inverse of the given number using its definition i.e. two numbers are multiplicative inverses if the product of two is equals to one. So we take number say $b$ and translate the definition into algebraic expression i.e.
$ - \dfrac{8}{3} \times b = 1$
Divide the above equation by $ - \dfrac{8}{3}$ we have
$b = - \dfrac{3}{8}$
This is the multiplicative inverse of the given number.
Hence we have solve both additive and multiplicative inverses of the number $ - \dfrac{8}{3}$
Note: While solving the question we saw that multiplicative inverse of a number is nothing but the reciprocal of the number and we could also solve it using cross multiplication method where we multiply components of a fraction upside-down in the other part of the equation like shown in the below figure –
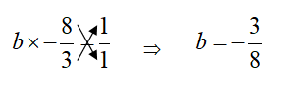
Complete solution step by step:
Firstly we write down the number of which we want to find the additive and multiplicative inverses i.e.
$ - \;\dfrac{8}{3}$
We will find the additive inverse first using its definition i.e. two numbers are additive inverses if the sum of two is equals to zero. So we let a number to be $a$ and translating the definition into mathematical expression we have -
$ - \dfrac{8}{3} + a = 0$
Now we simply have to solve this algebraic equation to find the additive inverse so we transfer the constant part to the RHS of the equation to get -
$ \Rightarrow a = \dfrac{8}{3}$
This is the additive inverse of the given number.
Now we try to find the multiplicative inverse of the given number using its definition i.e. two numbers are multiplicative inverses if the product of two is equals to one. So we take number say $b$ and translate the definition into algebraic expression i.e.
$ - \dfrac{8}{3} \times b = 1$
Divide the above equation by $ - \dfrac{8}{3}$ we have
$b = - \dfrac{3}{8}$
This is the multiplicative inverse of the given number.
Hence we have solve both additive and multiplicative inverses of the number $ - \dfrac{8}{3}$
Note: While solving the question we saw that multiplicative inverse of a number is nothing but the reciprocal of the number and we could also solve it using cross multiplication method where we multiply components of a fraction upside-down in the other part of the equation like shown in the below figure –
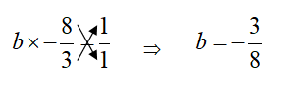
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

What are the controls affecting the climate of Ind class 7 social science CBSE

List of coprime numbers from 1 to 100 class 7 maths CBSE

Write a letter to the editor of the national daily class 7 english CBSE

Fill in the blanks with appropriate modals a Drivers class 7 english CBSE





