
Find the altitude of a rhombus whose area is 320 square meters and side is 5 m.
Answer
495k+ views
Hint: We will first draw a figure of rhombus (not to scale drawing) to look at this carefully. Now, we will use the formula of a rhombus related to its altitude and side and thus by putting in the values, get the required value.
Complete step-by-step answer:
Let us first look at the figure below.
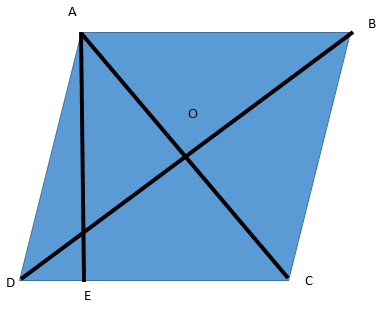
Here, in the rhombus above AB, BC, CD and DA are the sides of the rhombus which are given to be 5 m long.
We need to find the altitude AE’s length in this.
We know that the area of a rhombus is given by
Hence, after putting in the given values of area and side of the rhombus, we will thus get:-
Rearranging the terms, to get expression as follows:
On simplifying the values and calculation on RHS, we will get:-
The altitude of the rhombus is 64m.
Note: The students might make the mistake of not writing the unit after the answer is calculated. Just writing 64 does not make any sense. Thus, we definitely need to write 64 m.
Let us now look at the formula for a bit. It does seem to be exactly like a rectangle (Because height of a rhombus is equal to the width of rectangle only because all sides are perpendicular to each other in a rectangle)
Why this happens is because if we look at rhombus:
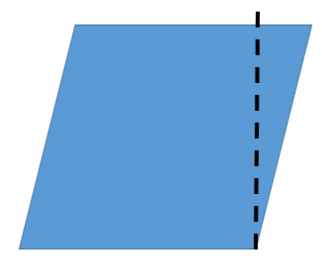
Now cutting off the area on the right of the dotted line and placing it on the left of the rhombus, we will get the following rectangle with length equal to the already given rhombus and the height of rhombus will become the breadth of the rectangle. So, if we multiply the breadth and the length, we will get the area of the rectangle which covers up the same amount of area as a rhombus.

Hence, their areas have similar formulas with a bit of modifications because they basically acquire equal area.
Complete step-by-step answer:
Let us first look at the figure below.

Here, in the rhombus above AB, BC, CD and DA are the sides of the rhombus which are given to be 5 m long.
We need to find the altitude AE’s length in this.
We know that the area of a rhombus is given by
Hence, after putting in the given values of area and side of the rhombus, we will thus get:-
Rearranging the terms, to get expression as follows:
On simplifying the values and calculation on RHS, we will get:-
The altitude of the rhombus is 64m.
Note: The students might make the mistake of not writing the unit after the answer is calculated. Just writing 64 does not make any sense. Thus, we definitely need to write 64 m.
Let us now look at the formula for a bit. It does seem to be exactly like a rectangle (Because height of a rhombus is equal to the width of rectangle only because all sides are perpendicular to each other in a rectangle)
Why this happens is because if we look at rhombus:

Now cutting off the area on the right of the dotted line and placing it on the left of the rhombus, we will get the following rectangle with length equal to the already given rhombus and the height of rhombus will become the breadth of the rectangle. So, if we multiply the breadth and the length, we will get the area of the rectangle which covers up the same amount of area as a rhombus.

Hence, their areas have similar formulas with a bit of modifications because they basically acquire equal area.
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

List some examples of Rabi and Kharif crops class 8 biology CBSE

How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

Advantages and disadvantages of science

How many ten lakhs are in one crore-class-8-maths-CBSE




