Question

How do you find the amplitude and period for \[y=\dfrac{1}{2}\cos x-3\]?

Answer 1

Hint: Compare the given cosine function with \[y=A\cos \left( Bx+C \right)+D\], where A = amplitude, B = coefficient of angle x, C = Phase shift and D = vertical shift. Now, use the formula: - amplitude = \[\left| A \right|\] and period = \[\dfrac{T}{\left| B \right|}\] to get the answer. Here, T = period of the cosine function = \[2\pi \].

Complete step-by-step solution:
Here, we have been provided with the cosine function \[y=\dfrac{1}{2}\cos x-3\] and we are asked to determine the amplitude and period of this function. But first let us understand both the terms one – by – one.
1. Amplitude: - Amplitude of a function is defined as the minimum or maximum displacement of the function from its mean position.
2. Period: - Period of a function is defined as the value / interval after which the value of the function starts repeating itself.
Now, let us come to the question. We have the cosine function \[y=\dfrac{1}{2}\cos x-3\]. Comparing this function with the general form given as: - \[y=A\cos \left( Bx+C \right)+D\], we have,
\[\left| A \right|\] = Amplitude = \[\left| \dfrac{1}{2} \right|=\dfrac{1}{2}\]
B = coefficient of x = 1
C = Phase shift = 0
D = vertical shift = -3
So, here the amplitude is \[\dfrac{1}{2}\], that means from the mean position the graph of the function y will be displaced up to a unit of \[\dfrac{1}{2}\] in both positive and negative direction. The reason is that cosine function lies in the interval [-1, 1], so its amplitude is 1.
\[\begin{align}
  & \Rightarrow -1\le \cos x\le 1 \\
 & \Rightarrow \dfrac{-1}{2}\le \dfrac{1}{2}\cos x\le \dfrac{1}{2} \\
\end{align}\]
Therefore, Amplitude = \[\dfrac{1}{2}\].
Now, let us determine the period of the given function y. Now, the period of the general equation: - \[y=A\cos \left( Bx+C \right)+D\] is given as: - Period = \[\dfrac{T}{\left| B \right|}\], where ‘T’ is the period of the cosine function. To determine the value of ‘T’ let us draw the graph of the cosine function. So, we have,

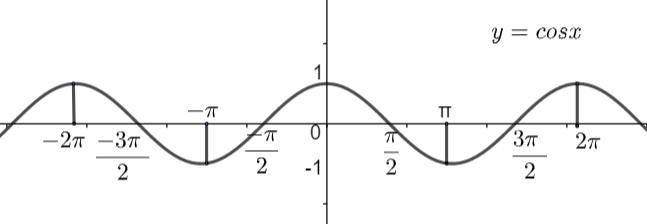
From the above graph we can clearly see that the value of \[y=\cos x\] starts repeating itself after an interval of the angle \[x=2\pi \], so we can say that the period of \[\cos x\] is \[2\pi \].
\[\Rightarrow T=2\pi \]
Now, the period of the cosine function provided to us, i.e., \[y=\dfrac{1}{2}\cos x-3\] can be given as: -
\[\Rightarrow \] Period = \[\dfrac{T}{\left| B \right|}\]
Substituting the values of T and B, we get,
\[\Rightarrow \] Period = \[\dfrac{2\pi }{\left| 1 \right|}\]
\[\Rightarrow \] Period = \[2\pi \].

Note: One may note that the phase shift ‘C’ and vertical shift ‘D’ do not have any effect on the amplitude or period of the function. However, the vertical shift can change the range of the function. Range means minimum and maximum value of y. You can similarly apply the same approach for the sine function: - \[y=A\sin \left( Bx+C \right)+D\] and the tangent function: - \[y=A\tan \left( Bx+C \right)+D\]. Remember that for sine function we have \[T=2\pi \] and for tangent function we have \[T=\pi \].