
How do you find the amplitude, period, and phase shift of
Answer
462.9k+ views
Hint: These types of trigonometric problems are pretty easy to solve and they are very straight forward. To find the amplitude, period and other things we first need to define the general equation of
Complete step by step answer: Now we start off our given solution, by writing the general form of the equation,
From
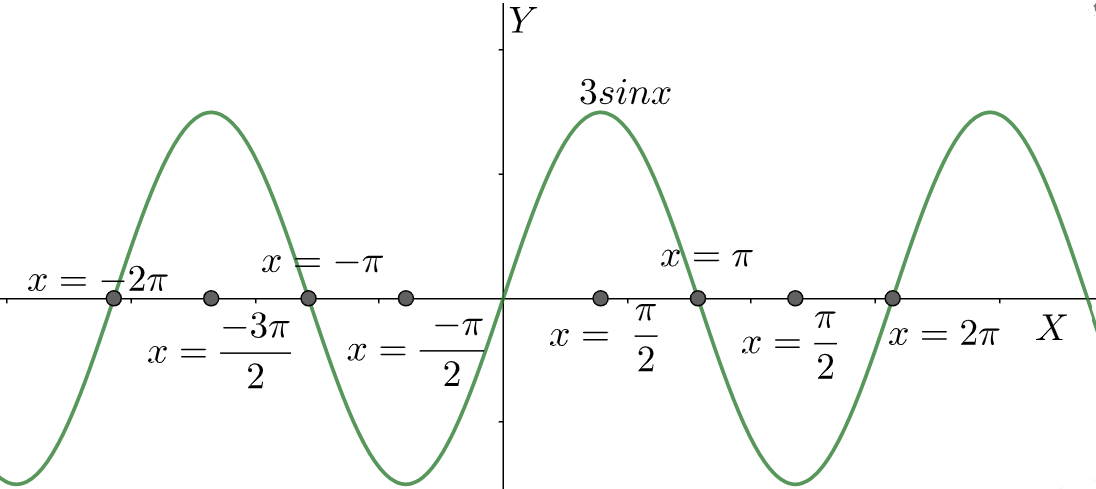
Now, writing our given equation of the form of the general defined one we get,
From this equation, we can write, that the Amplitude of the function is defined as,
We can also conclude that the value of the period of the function is defined as,
We can conclude that the value of the phase shift or the horizontal shift of the function is given by,
Note: While solving these types of problems, we must be very careful in representing the general form of the equation properly. Once the general form is represented correctly, we can find all the necessary things by comparing the given equation with the general form. We also need to remember all the variables and parameters, and what variables represent what.
Complete step by step answer: Now we start off our given solution, by writing the general form of the equation,
From

Now, writing our given equation of the form of the general defined one we get,
From this equation, we can write, that the Amplitude of the function is defined as,
We can also conclude that the value of the period of the function is defined as,
We can conclude that the value of the phase shift or the horizontal shift of the function is given by,
Note: While solving these types of problems, we must be very careful in representing the general form of the equation properly. Once the general form is represented correctly, we can find all the necessary things by comparing the given equation with the general form. We also need to remember all the variables and parameters, and what variables represent what.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




