
Find the angle

Answer
483.3k+ views
Hint: We will use the property of the exterior angle to obtain an equation with the angles
Complete step by step answer:
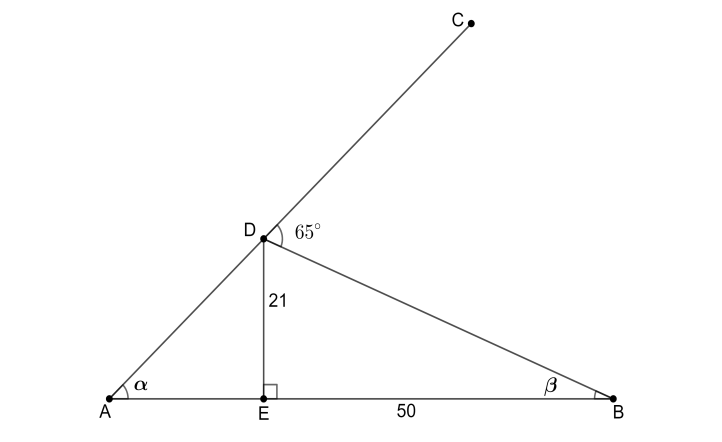
From the figure, we are given that
Substituting the values of these three angles from the figure, we get
Now, let us consider the right angled triangle
Substituting the values
Hence, we get the value of angle
Note:
It is important that we understand the geometry of a given figure. The concepts of exterior angles and interior angles are useful for such type of questions. We should know the definition of trigonometric functions since they can be used to obtain the values of angles by looking at the inverse trigonometric functions.
Complete step by step answer:
From the figure, we are given that
Substituting the values of these three angles from the figure, we get
Now, let us consider the right angled triangle
Substituting the values
Hence, we get the value of angle
Note:
It is important that we understand the geometry of a given figure. The concepts of exterior angles and interior angles are useful for such type of questions. We should know the definition of trigonometric functions since they can be used to obtain the values of angles by looking at the inverse trigonometric functions.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 10 biology CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




