Question

How to find the angle measure of the missing angle for a quadrilateral with angle measures of 145 degrees, 85 degrees and 45 degrees?

Answer 1

Hint: We know that, sum of all the angles of a quadrilateral is $360^0$. Here we have 3 angles. We need to find the fourth angle. So we will use this concept to find the fourth angle.

Complete step-by-step answer:
Here in the given figure I have shown a quadrilateral with vertex A, B, C and D where the angles are $\angle A = {85^ \circ }$ , $\angle B = {145^ \circ }$and $\angle C = {45^ \circ }$. Now and we just need to find the angle $\angle D$

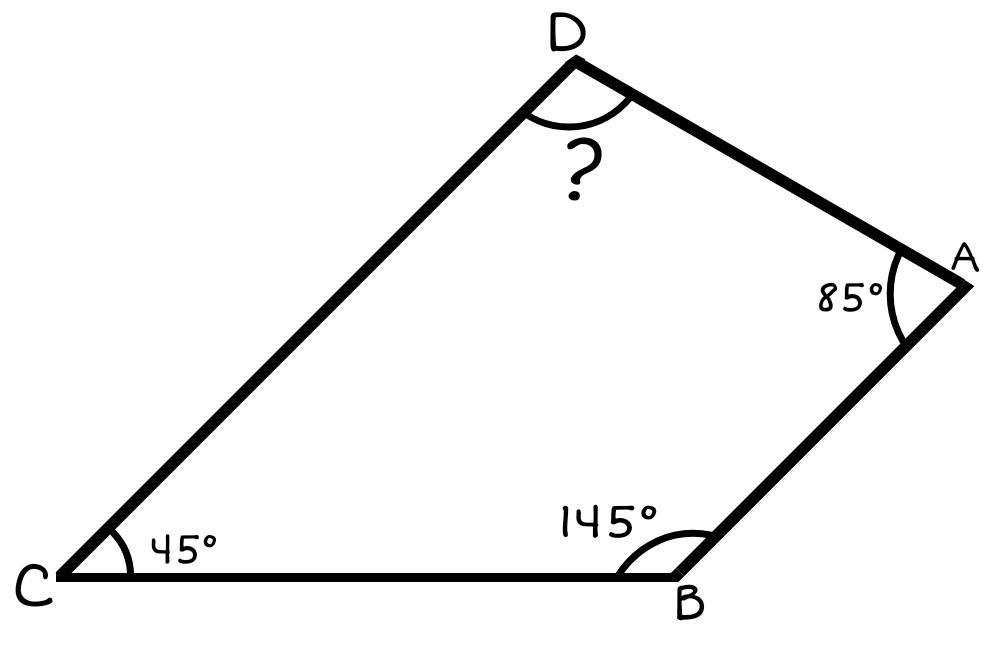
So in any kind of polygon whether it’s a regular or not the total sum of all the angles remains the same. For example, the sum of all the angles of a triangle ${180^ \circ }$ is and sum of all the angles of a pentagon is ${540^ \circ }$
Now the sum of all the angles of a quadrilateral is ${360^ \circ }$
Now the sum of $\angle A$, $\angle B$, $\angle C$ and $\angle D$is ${360^ \circ }$
$\angle A + \angle B + \angle C + \angle D = {360^ \circ }$
Now by substituting the values of $\angle A = {85^ \circ }$ , $\angle B = {145^ \circ }$and $\angle C = {45^ \circ }$in the above equation we get:
${85^ \circ } + {145^ \circ } + {45^ \circ } + \angle D = {360^ \circ }$
$\angle D = {360^ \circ } - \left( {{{85}^ \circ } + {{145}^ \circ } + {{45}^ \circ }} \right)$
$\angle D = {360^ \circ } - \left( {{{265}^ \circ }} \right)$
$\angle D = {95^ \circ }$
After solving the equation we get the value of $\angle D = {95^ \circ }$. So the value of the missing angle of the quadrilateral is ${95^ \circ }$( 95 degrees ).

Note: Once we get the sum of all the angles, we subtract the given angles to get the missing angle. It doesn’t matter if the shape (or polygon) given is an odd type of a convex type the sum of all the angles remains the same for all the given cases.