Question

Find the angle of projection for which the maximum height of the projectile is double the horizontal range attained by the body

Answer 1

Hint: In the above question it is asked to calculate the angle of projection under some given circumstances. For that we have to equate the expression for height of the projectile to twice the range(horizontal distance) covered by the projectile. Let us assume that this projection of the body takes place in vacuum i.e. no air is present that might offer air drag to the projectile.

Complete answer:
To begin with let us first draw the above projection of the projectile for better visualization.

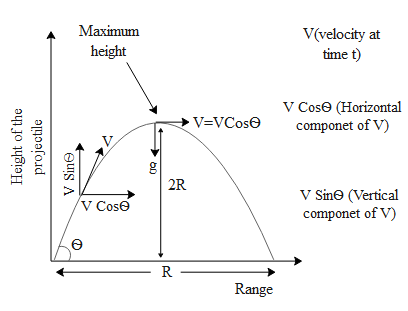
If we see the above figure we can clearly see that the height of the projectile is twice the range of the projectile. Let us say the time taken by the projectile to reach its maximum height is T. Therefore the total time of flight is 2T. The maximum height achieved by a projectile ignoring the air resistance is given by ${{\text{H}}_{\text{M}}}\text{=}\dfrac{{{\text{U}}^{\text{2}}}\text{Si}{{\text{n}}^{\text{2}}}\text{ }\!\!\theta\!\!\text{ }}{\text{2g}}...(1)$ where U is the initial velocity, $\theta $ is the angle of projection and g is the acceleration due to gravity. The horizontal distance covered by the projectile i.e. range is given by, $\text{R=}\dfrac{{{\text{U}}^{\text{2}}}\text{Sin2 }\!\!\theta\!\!\text{ }}{\text{g}}...(2)$.We want to calculate the angle of projection for the condition i.e.

${{H}_{M}}=2R...(3)$ Hence substituting equation 1 and 2 in 3 we get,
$\dfrac{{{\text{U}}^{\text{2}}}\text{Si}{{\text{n}}^{\text{2}}}\text{ }\!\!\theta\!\!\text{ }}{\text{2g}}=\dfrac{{{\text{U}}^{\text{2}}}\text{Sin2 }\!\!\theta\!\!\text{ }}{\text{g}}$ Further after cancelling the similar terms we get,

$\begin{align}
  & \dfrac{\text{Si}{{\text{n}}^{\text{2}}}\text{ }\!\!\theta\!\!\text{ }}{\text{2}}=\text{Sin2 }\!\!\theta\!\!\text{ , since Sin2 }\!\!\theta\!\!\text{ =2Sin }\!\!\theta\!\!\text{ Cos }\!\!\theta\!\!\text{ } \\
 & \dfrac{\text{Si}{{\text{n}}^{\text{2}}}\text{ }\!\!\theta\!\!\text{ }}{\text{2}}=\text{2Sin }\!\!\theta\!\!\text{ Cos }\!\!\theta\!\!\text{ } \\
 & \dfrac{\text{Sin }\!\!\theta\!\!\text{ }}{\text{Cos }\!\!\theta\!\!\text{ }}=4 \\
\end{align}$
Since $\dfrac{\text{Sin }\!\!\theta\!\!\text{ }}{\text{Cos }\!\!\theta\!\!\text{ }}=\tan \theta $
$\begin{align}
  & \text{Tan }\!\!\theta\!\!\text{ =4 hence} \\
 & \text{ }\!\!\theta\!\!\text{ =Ta}{{\text{n}}^{\text{-1}}}\text{4=36}\text{.8}{{\text{6}}^{\text{o}}} \\
\end{align}$

Hence the angle of projection should be 36.86 degrees.

Note:
In the real world the angle of projection required to satisfy the above condition should have been slightly greater as the range would have been less due to air resistance. One more important fact is that for a given range the maximum height of the projectile can have two different values. This depends on the angle of projection.