Question

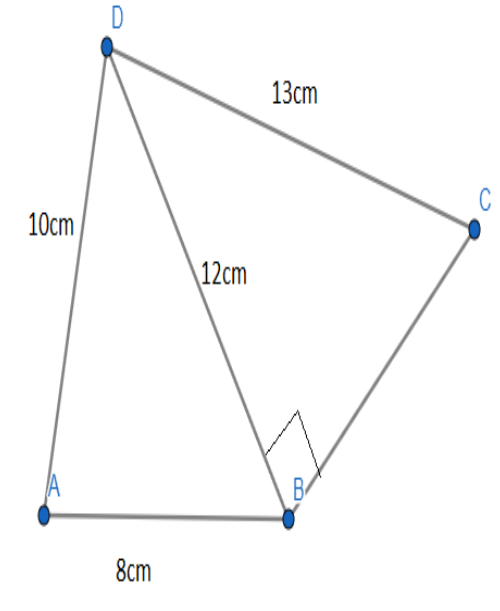
Find the area and the perimeter of quadrilateral ABCD, given below; if AB= 8cm, AD=10cm, BD =12cm, DC =13cm and $\angle \text{DBC}={{90}^{\circ }}$ \[\]

Answer 1

Hint: We find the length of the side BC using Pythagoras theorem in the right-angled triangle DBC. We find the area of the triangle ABC using the formula for area with semi-perimeter $s$ and length of the sides $a,b,c$ as $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$. We find the area of the triangle DBC with base $b$ and height $h$ using the formula $\dfrac{1}{2}\times b\times h$. We add the areas of both the triangles to get the area of quadrilateral ABCD and add the lengths of all the sides of quadrilateral ABCD to get its perimeter.

Complete step-by-step solution:
We are given the figure of the quadrilateral ABCD which were the diagonal BD divides the quadrilateral ABCD into two triangles. The first triangle is an acute-angled triangle ABD with the length of all three sides given to us as AB= 8 cm, AD=10 cm, BD =12cm. The second triangle is right-angled triangle DBC where right angle is $\angle DBC={{90}^{\circ }}$ and lengths of the sides are given to us as BD=12cm,CD=13cm.\[\]
We know Pythagoras theorem states that “In a right-angled triangle the square of the hypotenuse is the sum of squares of other two sides”. So in right-angled triangle DBC, we use Pythagoras theorem and find the length of BC as,
\[\begin{align}
  & D{{C}^{2}}=B{{D}^{2}}+B{{C}^{2}} \\
 & \Rightarrow B{{C}^{2}}=B{{D}^{2}}-D{{C}^{2}} \\
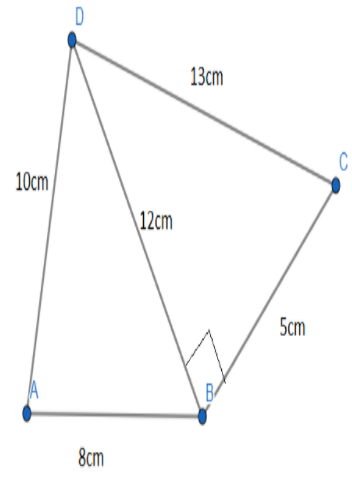
 & \Rightarrow BC=\sqrt{B{{D}^{2}}-D{{C}^{2}}}=\sqrt{{{\left( 13\text{cm} \right)}^{2}}-{{\left( 12\text{cm} \right)}^{2}}} \\
 & \Rightarrow BC=\sqrt{25\text{c}{{\text{m}}^{2}}}=5\text{cm} \\
\end{align}\]

The semi-perimeter of the triangle ABD is
\[s=\dfrac{AB+BD+DA}{2}=\dfrac{8+12+10}{2}=15\text{cm}\]
We use the formula for area of triangle with semi-perimeter and sides to find the area of triangle ABC in square cm as
\[\begin{align}
& \text{Area of }\Delta \text{ABD}=\sqrt{s\left( s-AB \right)\left( s-BD \right)\left( s-AD \right)} \\
 & =\sqrt{15\left( 15-10 \right)\left( 15-12 \right)\left( 15-8 \right)} \\
 & =\sqrt{15\times 5\times 3\times 7}=15\sqrt{7} \\
\end{align}\]
We find the area of the triangle with base and height to find the area of triangle DBC with base BC and height BD in square cm as
\[\text{Area of }\Delta \text{DBC}=\dfrac{1}{2}\times BC\times BD=\dfrac{1}{2}\times 5\times 12=30\]
The area of the quadrilateral ABCD is the sum areas of the triangles ABD and DBC. So we have,
\[\begin{align}
  & \text{Area of ABCD}=\text{Area of }\Delta \text{ABD}+\text{Area of }\Delta \text{DBC} \\
&\Rightarrow \text{Area of ABCD=30+15}\sqrt{7}=30+15\times 2.64=30+39.4=69.4\text{c}{{\text{m}}^{2}} \\
\end{align}\]
The perimeter of the quadrilateral ABCD is the sum of lengths of its sides. So we have
\[\begin{align}
  & \text{Perimeter of ABCD}=AB+BC+CD+AD \\
 & \Rightarrow \text{Perimeter of ABCD}=8+5+13+10=36\text{cm} \\
\end{align}\]

Note: We note that we have rejected negative square roots for BC and area of triangle ABD as length and area are always positive. We also note that we cannot find the area of quadrilateral directly unless it is a parallelogram where an altitude with length $h$ is dropped from a vertex to the opposite side of length $b$ and the area is $b\times h$.