Questions & Answers
Question
Answers
Related Questions
Find the area bounded by the ellipse \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] and the ordinates $x = 0$and $x = ae$, where ${b^2} = {a^2}\left( {1 - {e^2}} \right)$ and $e < 1$.
Answer
![Verified]()
Verified
Verified
Hint: Simplify the given ellipse equation and integrate within the given ordinate limits to find the area.
An ellipse of the form \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] will meet the X-axis at (a, 0) and the Y-axis at (0, b). Let these points be P (a,0) and Q (0, b). It is symmetrical about the axes.
The ordinates given are $x = 0$and $x = ae$ which will be parallel to the Y-axis as shown in the figure.
The shaded area is the area bounded by the ellipse and the given ordinates.
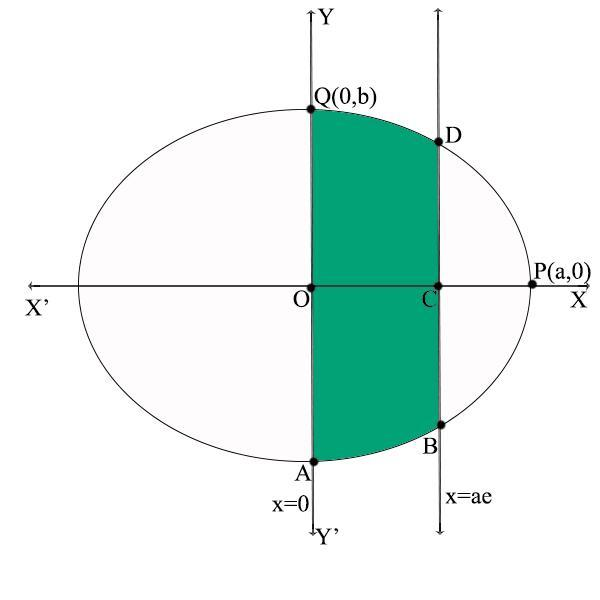
Required area = Area of the shaded region
= $2 \times $Area of QOCD
=$2 \times \int_0^{ae} y dx$ …(1)
The given equation is \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\]. Let us find the value of y from this equation and substitute in equation (1).
$\begin{gathered}
\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1 \\
\begin{array}{*{20}{l}}
\begin{gathered}
\dfrac{{{y^2}}}{{{b^2}}} = 1 - \dfrac{{{x^2}}}{{{a^2}}} \\
\dfrac{{{y^2}}}{{{b^2}}} = \dfrac{{{a^2} - {x^2}}}{{{a^2}}} \\
\end{gathered} \\
{{y^2} = \dfrac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {x^2}} \right)} \\
{y = \pm \sqrt {\dfrac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {x^2}} \right)} } \\
{y = \pm \dfrac{b}{a}\sqrt {\left( {{a^2} - {x^2}} \right)} }
\end{array} \\
\end{gathered} $
Since, the area in equation (1) which is the area of QOCD is in the 1st quadrant. Hence, the value of y will be positive.
Hence, $y = \dfrac{b}{a}\sqrt {\left( {{a^2} - {x^2}} \right)} $ …(2)
Substituting (2) in (1),
Required area =$2 \times \int_0^{ae} y dx$
\[\begin{array}{*{20}{l}}
{ = 2\mathop \smallint \limits_0^{ae} \dfrac{b}{a}\sqrt {{a^2} - {x^2}} dx} \\
{ = \dfrac{{2b}}{a}\mathop \smallint \limits_0^{ae} \sqrt {{a^2} - {x^2}} dx}
\end{array}\] (Since a and b are constants)
We know that, \[\mathop \smallint \nolimits^ \sqrt {{a^2} - {x^2}} dx = \dfrac{{x\sqrt {{a^2} - {x^2}} }}{2} + \dfrac{{{a^2}}}{2}{\sin ^{ - 1}}(\dfrac{x}{a}) + c\]
Using this in the previous step, we get
Required area = \[\dfrac{{2b}}{a}[\dfrac{1}{2}x\sqrt {{a^2} - {x^2}} + \dfrac{{{a^2}}}{2}{\sin ^{ - 1}}\dfrac{x}{a}]_0^{ae}\] \[\begin{gathered}
\begin{array}{*{20}{l}}
{ = \dfrac{{2b}}{a}[(\dfrac{{ae}}{2}\sqrt {{a^2} - {{(ae)}^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}\dfrac{{ae}}{a}) - (\dfrac{0}{2}\sqrt {{a^2} - 0} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(\dfrac{0}{a}))]} \\
{ = \dfrac{{2b}}{a}[\dfrac{{ae}}{2}\sqrt {{a^2} - {a^2}{e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(e) - 0 - \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(0)]} \\
{ = \dfrac{{2b}}{a}[\dfrac{{ae}}{2} \cdot a\sqrt {1 - {e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}e - 0]}
\end{array} \\
\begin{array}{*{20}{l}}
{ = \dfrac{{2b}}{a}[\dfrac{{{a^2}e}}{2}\sqrt {1 - {e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}e]} \\
{ = \dfrac{{2b}}{a}(\dfrac{{{a^2}}}{2})[e\sqrt {1 - {e^2}} + {{\sin }^{ - 1}}e]} \\
{ = ab[e\sqrt {1 - {e^2}} + {{\sin }^{ - 1}}e]}
\end{array} \\
\end{gathered} \]
Required Area bounded by the ellipse \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] and the ordinates $x = 0$and $x = ae$
\[ = ab[e\sqrt {1 - {e^2}} + {\sin ^{ - 1}}e]\]
Note: The required area can also be found by integrating the entire shaded area QOABCD instead of finding $2 \times $Area of QOCD. It would be a little lengthier and more unnecessary because the given ellipse is symmetrical about the origin.
An ellipse of the form \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] will meet the X-axis at (a, 0) and the Y-axis at (0, b). Let these points be P (a,0) and Q (0, b). It is symmetrical about the axes.
The ordinates given are $x = 0$and $x = ae$ which will be parallel to the Y-axis as shown in the figure.
The shaded area is the area bounded by the ellipse and the given ordinates.
Required area = Area of the shaded region
= $2 \times $Area of QOCD
=$2 \times \int_0^{ae} y dx$ …(1)
The given equation is \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\]. Let us find the value of y from this equation and substitute in equation (1).
$\begin{gathered}
\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1 \\
\begin{array}{*{20}{l}}
\begin{gathered}
\dfrac{{{y^2}}}{{{b^2}}} = 1 - \dfrac{{{x^2}}}{{{a^2}}} \\
\dfrac{{{y^2}}}{{{b^2}}} = \dfrac{{{a^2} - {x^2}}}{{{a^2}}} \\
\end{gathered} \\
{{y^2} = \dfrac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {x^2}} \right)} \\
{y = \pm \sqrt {\dfrac{{{b^2}}}{{{a^2}}}\left( {{a^2} - {x^2}} \right)} } \\
{y = \pm \dfrac{b}{a}\sqrt {\left( {{a^2} - {x^2}} \right)} }
\end{array} \\
\end{gathered} $
Since, the area in equation (1) which is the area of QOCD is in the 1st quadrant. Hence, the value of y will be positive.
Hence, $y = \dfrac{b}{a}\sqrt {\left( {{a^2} - {x^2}} \right)} $ …(2)
Substituting (2) in (1),
Required area =$2 \times \int_0^{ae} y dx$
\[\begin{array}{*{20}{l}}
{ = 2\mathop \smallint \limits_0^{ae} \dfrac{b}{a}\sqrt {{a^2} - {x^2}} dx} \\
{ = \dfrac{{2b}}{a}\mathop \smallint \limits_0^{ae} \sqrt {{a^2} - {x^2}} dx}
\end{array}\] (Since a and b are constants)
We know that, \[\mathop \smallint \nolimits^ \sqrt {{a^2} - {x^2}} dx = \dfrac{{x\sqrt {{a^2} - {x^2}} }}{2} + \dfrac{{{a^2}}}{2}{\sin ^{ - 1}}(\dfrac{x}{a}) + c\]
Using this in the previous step, we get
Required area = \[\dfrac{{2b}}{a}[\dfrac{1}{2}x\sqrt {{a^2} - {x^2}} + \dfrac{{{a^2}}}{2}{\sin ^{ - 1}}\dfrac{x}{a}]_0^{ae}\] \[\begin{gathered}
\begin{array}{*{20}{l}}
{ = \dfrac{{2b}}{a}[(\dfrac{{ae}}{2}\sqrt {{a^2} - {{(ae)}^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}\dfrac{{ae}}{a}) - (\dfrac{0}{2}\sqrt {{a^2} - 0} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(\dfrac{0}{a}))]} \\
{ = \dfrac{{2b}}{a}[\dfrac{{ae}}{2}\sqrt {{a^2} - {a^2}{e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(e) - 0 - \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}(0)]} \\
{ = \dfrac{{2b}}{a}[\dfrac{{ae}}{2} \cdot a\sqrt {1 - {e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}e - 0]}
\end{array} \\
\begin{array}{*{20}{l}}
{ = \dfrac{{2b}}{a}[\dfrac{{{a^2}e}}{2}\sqrt {1 - {e^2}} + \dfrac{{{a^2}}}{2}{{\sin }^{ - 1}}e]} \\
{ = \dfrac{{2b}}{a}(\dfrac{{{a^2}}}{2})[e\sqrt {1 - {e^2}} + {{\sin }^{ - 1}}e]} \\
{ = ab[e\sqrt {1 - {e^2}} + {{\sin }^{ - 1}}e]}
\end{array} \\
\end{gathered} \]
Required Area bounded by the ellipse \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] and the ordinates $x = 0$and $x = ae$
\[ = ab[e\sqrt {1 - {e^2}} + {\sin ^{ - 1}}e]\]
Note: The required area can also be found by integrating the entire shaded area QOABCD instead of finding $2 \times $Area of QOCD. It would be a little lengthier and more unnecessary because the given ellipse is symmetrical about the origin.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
.png)
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
JEE Main & Advanced 2023
-
-
NEET
-
NEET 2021
-
NEET 2022
-
NEET 2023
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Micro Courses
-
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
