Question

Find the area enclosed by each of the given figures:

Answer 1

Hint: To specify a figure most fundamental quantities are perimeter, area and volume. Perimeter can be defined as the total length of the boundary of a geometrical figure. Area can be defined as the space occupied by a flat shape or the surface of an object. Area of a combination of two figures is the individual area of each figure. So, using this definition we can easily solve our problem.

Complete step-by-step answer:
According to our question, we are given three figures whose areas are to be evaluated. Some of the useful formulas for calculating area of geometrical figures are:
Area of a square of side a $={{a}^{2}}$
Area of a triangle having base length b and height h $=\dfrac{1}{2}\times b\times h$
Area of a trapezium of height h and parallel sides a and b $=\dfrac{h}{2}\left( a+b \right)$
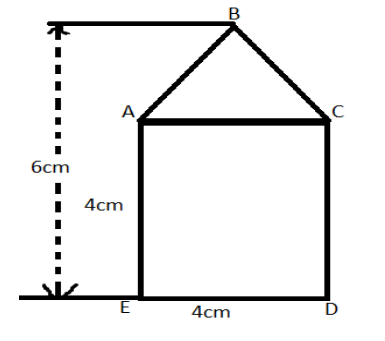
For figure 1, area of the polygon is equal to sum of the area of square of side 4 cm and triangle having base 4 cm and height 2 cm:
$\begin{align}
  & =4\times 4+\dfrac{1}{2}\times 4\times 2 \\
 & =16+4 \\
 & =20c{{m}^{2}} \\
\end{align}$
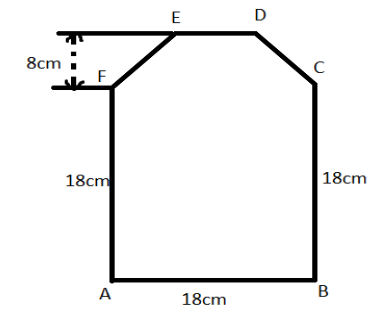
For figure 2, area of the polygon is equal to sum of area of square of side 18 cm and trapezium of height 8 cm and parallel sides 18 cm and 8 cm:
$\begin{align}
  & =18\times 18+\dfrac{8}{2}\left( 8+18 \right) \\
 & =324+4(26) \\
 & =324+104 \\
 & =428c{{m}^{2}} \\
\end{align}$
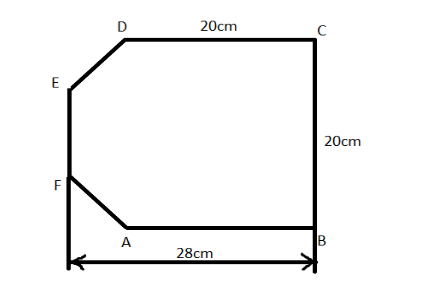
For figure 3, area of the polygon is equal to sum of area of square of side 20 cm and trapezium of height 8 cm and parallel sides 20 cm and 8 cm:
$\begin{align}
  & =20\times 20+\dfrac{8}{2}\times \left( 8+20 \right) \\
 & =400+4\times 28 \\
 & =400+112 \\
 & =512c{{m}^{2}} \\
\end{align}$
Area of figure (i) is 20 square cm.
Area of figure (ii) is 428 square cm.
Area of figure (iii) is 512 square cm.

Note: The key concept for solving this problem is the segregation of the whole area into two parts. By separating the area into desired shapes, we easily evaluated the area of the whole polygon. This concept is very useful in solving complex problems.