Question

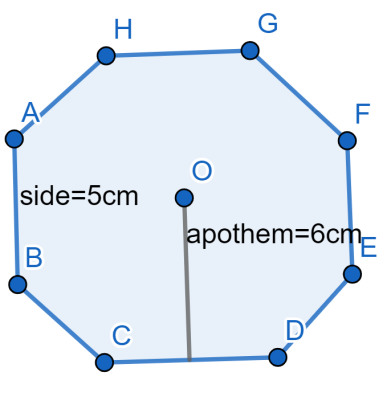
How do you find the area of a regular octagon with side length $5cm$ and apothem $6cm$ ?

Answer 1

Hint: For answering this question we have been asked to find the area of a regular octagon with side length $5cm$ and apothem $6cm$ . From the basics we know that we have a formula for finding the area of regular octagon which is mathematically given as $\dfrac{1}{2}\times perimeter\times apothem\Rightarrow 8\left( side\text{ length} \right)\left( apothem\times \dfrac{1}{2} \right)$ .

Complete step by step solution:
Now considering from the question we have been asked to find the area of a regular octagon with side length $5cm$ and apothem $6cm$ .
From the basics of concept we know that we have a formula for finding the area of regular octagon which is mathematically given as $\dfrac{1}{2}\times perimeter\times apothem\Rightarrow 8\left( side\text{ length} \right)\left( apothem\times \dfrac{1}{2} \right)$ .

We will use this formula for finding the area of the given polygon.
By applying we will have
$Area=8\left( side\text{ length} \right)\left( apothem\times \dfrac{1}{2} \right)\Rightarrow \dfrac{1}{2}\times 8\times 5\times 6$
By further simplifying by performing some basic arithmetic calculations we will have $\Rightarrow 120c{{m}^{2}}$ .
Therefore we can conclude that the area of a regular octagon with side length $5cm$ and apothem $6cm$ is given as $120c{{m}^{2}}$ .

Note: While answering questions of this type we should be sure with our concepts we apply and the calculations we perform during this process. If we are aware of the formula then this is a very simple question and can be done in a short span of time and very few mistakes are possible. We can find the perimeter of a regular octagon by multiplying the side length with $8$ mathematically given as $8\left( side\text{ length} \right)$ . For this question it means for the perimeter of the regular octagon given is $8\times 5=40cm$ .