Question

How do you find the area of an equilateral triangle with a given apothem?

Answer 1

Hint: The apothem of an equilateral triangle can be expressed as the short leg of a $ 30 - 60 - 90 $ triangle and where the long leg is equal to $ s/2 $ . We will draw the diagram and will find accordingly the area of an equilateral triangle. Note equilateral triangle is the triangle with the equal measures of sides with equal angles.

Complete step-by-step answer:

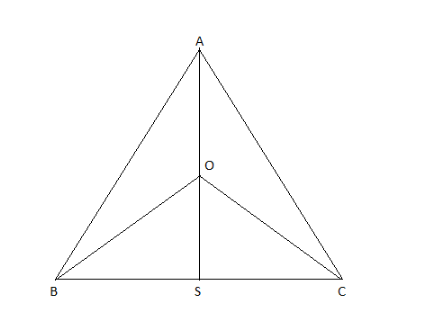
We know that the area of the apothem is $ a = \dfrac{s}{{2.\sqrt 3 }} $
Where “S” is the length of the side of an equilateral triangle.
Do cross – multiplication in the above equation, where numerator of one part is multiplied with the denominator of the opposite side.
 $ \Rightarrow a(2.\sqrt 3 ) = s $
It can be re-written as –
 $ \Rightarrow s = a(2.\sqrt 3 ) $ …. (A)
Now, the area of the equilateral triangle can be expressed as –
 $ {A_t} = \dfrac{{\sqrt 3 {s^2}}}{4} $
Place the value of equation (A) in the above equation –
 $ {A_t} = \dfrac{{\sqrt 3 {{(a2.\sqrt 3 )}^2}}}{4} $
Simplify the above equation – Square and square root cancel each other in the above equation.
 $ {A_t} = \dfrac{{\sqrt 3 {a^2}.4.3}}{4} $
Common factors from the numerator and the denominator cancel each other. Remove from the numerator and the denominator.
 $ \Rightarrow {A_t} = 3\sqrt 3 {a^2} $
This is the required solution.
So, the correct answer is “ $ 3\sqrt 3 {a^2} $ ”.

Note: Remember the standard formulas for the areas of the area equilateral triangle and the apothem. Be good in the concepts of the square and square-root, they both cancel each other. Square is the number multiplied by itself twice.
The area of the regular polygon can be expressed as the $ A = \dfrac{1}{2}p $ where A is the area and the p is the perimeter of the polygon.