Question

How do you find the area of an isosceles triangle with base 10 and perimeter 36?

Answer 1

Hint: Here in this question, we have to find the area of an isosceles triangle. We have value for one side of a triangle and the perimeter of an isosceles triangle. By using the property of isosceles triangle, we determine the other two sides of a triangle and hence we find the area of an isosceles triangle.

Complete step-by-step answer:

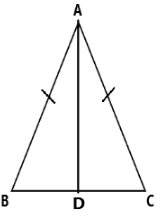
The isosceles triangle is a triangle whose two sides are equal. We have a base of the triangle and it is 10. Now consider the figure ABC is an isosceles triangle and length of BC is 10. The triangle is an isosceles triangle so we have AB=AC. The perimeter of an isosceles triangle is 36.
The perimeter of a triangle ABC is given by
 \[perimeter = AB + BC + AC\]
Substituting the values, we have
 \[ \Rightarrow 36 = AB + 10 + AB\]
Take 10 on LHS we get
 \[ \Rightarrow 36 - 10 = 2AB\]
 \[ \Rightarrow 26 = 2AB\]
Dividing by 2 we get
 \[ \Rightarrow AB = 13\]
Hence, we have obtained the value of AB.
Now we have to find the area of a triangle. The area of a triangle is given by \[\dfrac{1}{2} \times base \times height\]
We don’t know the value of height. To determine the height of the triangle, let we draw a perpendicular line from point A to BC. D is the midpoint of BC.
Therefore DC=5.
Consider the triangle ADC and apply Pythagoras theorem to it, therefore we have
 \[{(13)^2} = {5^2} + {x^2}\]
On simplifying we get
 \[ \Rightarrow 169 = 25 + {x^2}\]
Take 25 to LHS we get
 \[
   \Rightarrow 169 - 25 = {x^2} \\
   \Rightarrow 144 = {x^2} \;
 \]
Taking the square root we get
 \[ \Rightarrow x = 12\]
Since it is a measurement, we can’t take negative value. So, we take positive value.
Therefore, the height of a triangle is 12.
Now, the area of an isosceles triangle is \[\dfrac{1}{2} \times base \times height\]
Substituting all the values we have
 \[A = \dfrac{1}{2} \times 10 \times 12\]
On simplifying we get
 \[
   \Rightarrow A = 5 \times 12 \\
   \Rightarrow A = 60\;sq.units. \;
 \]
Therefore, the area of an isosceles triangle is 60 square units.
So, the correct answer is “60 square units”.

Note: The area of a triangle is given by \[\dfrac{1}{2} \times base \times height\] . This formula is applicable to all kinds of triangles. There is no change in formula at all. The perimeter is having the unit as a unit itself. The area as a unit as square units. The unit is most important and we should not forget to write it.