Question

Find the area of quadrilateral ABCD whose vertices are A(-3,-1), B(-2,-4), C(4,-1), and D(3,4).

Answer 1

Hint: To solve this question first we will plot the points and join the vertices with the adjacent vertices. After that, we will join the diagonal AC. Then, we will get two triangles and the sum of the areas of those two triangles will be equals to the area of quadrilateral ABCD.

Complete step-by-step solution:

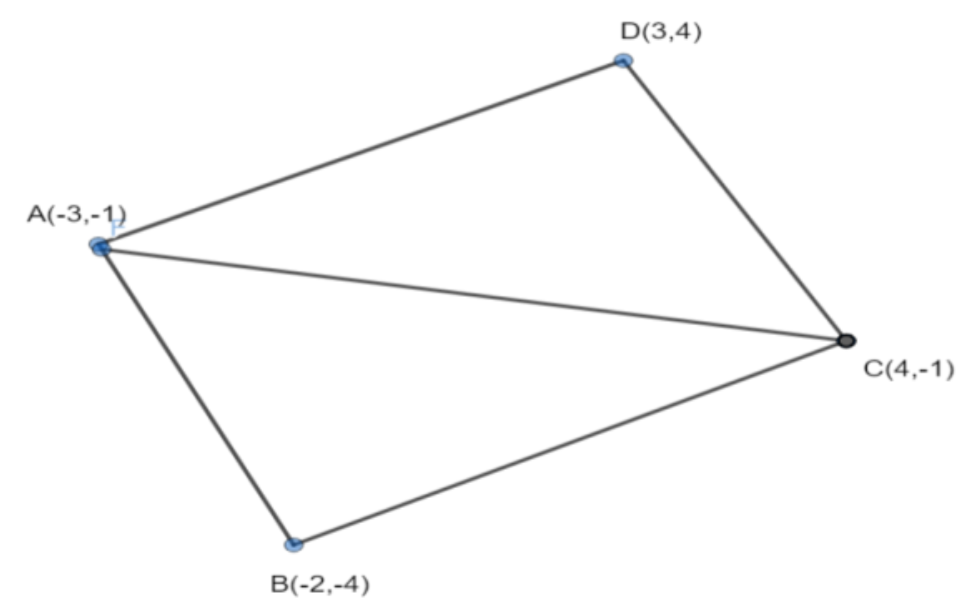
Now, the above figure is quadrilateral ABCD whose area is to be evaluated.
In question, it is given that vertices of a quadrilateral are A(-3,-1), B(-2,-4), C(4,-1), and D(3,4).
Now, what we will do is we will join points A and C with a straight line which is diagonal of quadrilateral ABCD.
From, the figure we can see that we have two triangles, triangle ABC and triangle ADC with base AC.
Now, we know that if we have triangle whose three vertices are A ( a, b ) , B ( c, d ) and C ( e, f ), then area of triangle is equal to, $\dfrac{1}{2}[a(d-f)+c(f-b)+e(b-d)]$.
For, triangle ABC, we have vertices A ( -3, -1 ), B ( -2, -4 ) and C ( 4, -1 ).
So, area of triangle ABC will be \[=\dfrac{1}{2}[-3(-4-(-1))+(-2)(-1-(-1))+4(-1-(-4))]\]
On solving, we get $\dfrac{1}{2}[9+0+12]$
on simplifying, we get
$\dfrac{1}{2}[21]=10.5$$c{{m}^{2}}$
For, triangle ADC, we have vertices A ( -3, -1 ), D ( 3, 4 ) and C ( 4, -1 ).
So, area of triangle ADC will be \[=\dfrac{1}{2}[-3(4-(-1))+3(-1-(-1))+4(-1-4)]\]
On solving, we get $\dfrac{1}{2}[-15+0-20]$
on simplifying, we get
$\dfrac{1}{2}[-35]=-17.5$$c{{m}^{2}}$
As, area cannot be negative , so
Area of triangle ADC = 17.5 $c{{m}^{2}}$
From figure we can see, Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ADC
So, Area of quadrilateral ABCD = 10.5 + 17.5 $c{{m}^{2}}$
On solving, we get
Area of quadrilateral ABCD = 28 $c{{m}^{2}}$

Note: Try to always solve the area of the quadrilateral by dividing it into two triangles by joining any one of the triangles. Always remember that if we have triangle whose three vertices are A ( a, b ) , B ( c, d ) and C ( e, f ), then area of triangle is equal to, $\dfrac{1}{2}[a(d-f)+c(f-b)+e(b-d)]$. Always put units after the final numerical answer. Try to avoid calculation mistakes.