Question

Find the area of the circle in which a square of area $64c{{m}^{2}}$ is inscribed. $\left( use\pi =3.14 \right).$ .

Answer 1

Hint: To solve this question, we will make use of the fact that the corner of the square touches the circle and also the diameter of the circle is equal to the length of diagonal of the square.

Complete step by step answer:
The square is inscribed in the circle is shown below:

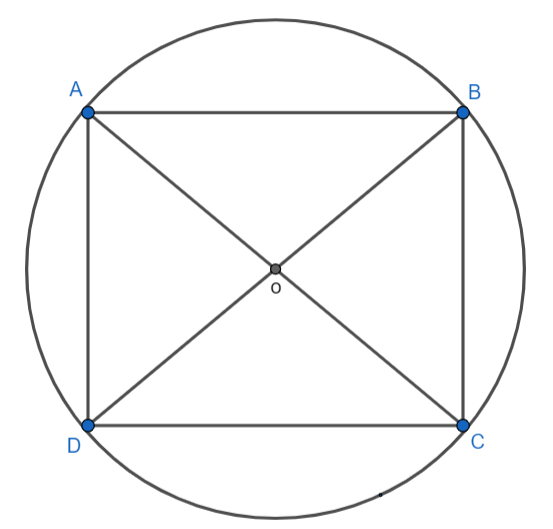
Here, we can see that the points A, B, C and D reside on the circumference of the circle o is the centre of the circle. It is given in the question that the square inscribed in the circle has an area of $64c{{m}^{2}}$ . Now, we have to determine the length of the side of the square.
This can be done by applying the formula of the area of the square. The area of the square is given by:
Area $={{\left( side \right)}^{2}}.$
$\Rightarrow 64={{\left( side \right)}^{2}}$
$\Rightarrow \left( side \right)=\sqrt{64}$
$\Rightarrow side=8cm.$
Thus the side of the square inscribed in the circle is = 8cm.
Now, we will calculate the length of the diagonal BD. We know that the angle between the sides BC and CD is ${{90}^{\circ }}$ . Here, we are going to consider the triangle BCD Now, we will apply the Pythagoras theorem in this triangle the Pythagoras theorem is given by:
${{H}^{2}}={{P}^{2}}+{{B}^{2}}$.
Where H is the hypotenuse, P is the perpendicular and B is the base. Here is our case, $H=BD,P=BC$ and $B=CD$ . Therefore, we get the following:
$\Rightarrow {{\left( BD \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( CD \right)}^{2}}$ .
$\Rightarrow {{\left( BD \right)}^{2}}={{\left( 8 \right)}^{2}}+{{\left( 8 \right)}^{2}}$ .
$\Rightarrow {{\left( BD \right)}^{2}}=64+64$ .
$\Rightarrow {{\left( BD \right)}^{2}}=128$ .
$\Rightarrow BD=\sqrt{128}$ .
$\Rightarrow BD=8\sqrt{2}cm$ .
Here, we can see that the length of diagonal BD is equal to the diameter of the circle. So, the diameter of the circle$=8\sqrt{2}cm$ . Therefore, the radius of the circle will be $=\dfrac{8\sqrt{2}}{2}=4\sqrt{2}cm$ Now, we have calculated the radius of the circle so we are going to calculate the area of the circle now.
The area of the circle is given by the formula:
Area $=\pi {{\left( radius \right)}^{2}}$ .
$\Rightarrow Area=\pi {{\left( 4\sqrt{2} \right)}^{2}}$ .
$\Rightarrow Area=\pi \left( 32 \right)$ .
$\Rightarrow Area=3.14\times 32$ .
$\Rightarrow Area=100.48c{{m}^{2}}$ .
Thus, the area of the circle $=100.48c{{m}^{2}}$ .

Note:
We can also calculate the radius of the circle as follows: we know that, area of the square is 4 times the area of triangle ADB. Thus the area of the triangle AOB is $\dfrac{64}{4}c{{m}^{2}}=16c{{m}^{2}}$ . Now we can also calculate the area of the triangle AOB by formula:
Area of $\Delta AOB=\dfrac{1}{2}\times AO\times BO\times \sin \left( \angle AOB \right)$
$\begin{align}
  & 16=\dfrac{1}{2}\times r\times r\times \sin \dfrac{\pi }{2} \\
 & 32={{r}^{2}} \\
 & \Rightarrow r=\sqrt{32}=4\sqrt{2}cm \\
\end{align}$