Question

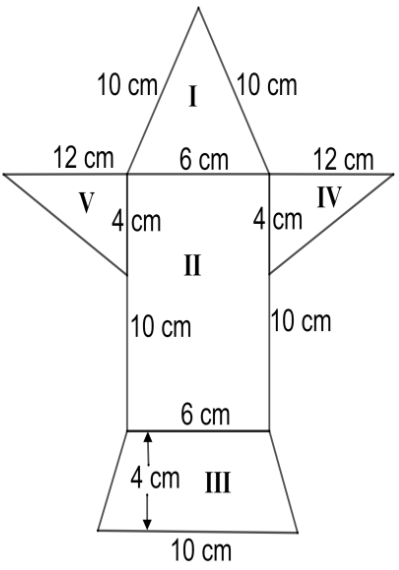
Find the area of the following figure:

Answer 1

Hint: The given figure consists of a combination of 5 different regions. Three of the regions are triangles. One region is a rectangle and the remaining region is a trapezium. We will use the formulae of the area of these shapes to find the area of the individual regions. We will find the area of the individual regions and then add these to get the desired area of the given figure.

Complete step-by-step solution
Let us find the area of region I. Region I is an isosceles triangle. We know that the altitude of this triangle will bisect the base. So, to find the height or altitude of this triangle we will use the Pythagoras theorem in the following manner,
${{\left( \dfrac{1}{2}\text{base} \right)}^{2}}+{{\left( \text{altitude} \right)}^{2}}={{\left( \text{side} \right)}^{2}}$
We know that the base is 6 cm and the side is 10 cm. Substituting these values, we get
${{\left( \dfrac{1}{2}\times 6 \right)}^{2}}+{{\left( \text{altitude} \right)}^{2}}={{10}^{2}}$
Simplifying this equation, we have
$\text{altitude = }\sqrt{100-9}=\sqrt{91}$
Now, the formula for the area of the triangle is $A\left( \text{triangle} \right)=\dfrac{1}{2}\times \text{base}\times \text{height}$. Substituting these values in the formula for the area of a triangle we get,
$\begin{align}
  & \text{Area of region I = }\dfrac{1}{2}\times 6\times \sqrt{91} \\
 & =3\sqrt{91}
\end{align}$
Now, from the given figure, we can see that region IV and region V are the two equal right angled triangles. The height for these triangles is 12 cm and the base is 4 cm. Substituting these values in the formula for the area of a triangle, we get
$\begin{align}
  & \text{Area of region IV = }\dfrac{1}{2}\times 4\times 12 \\
 & =24
\end{align}$
And, $\text{Area of region V = 24}$.
Next, we will find the area of the region II, which is a rectangle. The formula for the area of the rectangle is $A\left( \text{rectangle} \right)=\text{length}\times \text{breadth}$. The length of region II is 10 cm and the breadth is 6 cm. Substituting these values in the formula for the area of a rectangle, we get
\[\begin{align}
  & \text{Area of region II = 10}\times \text{6} \\
 & \text{= 60}
\end{align}\]
Now, we have to compute the area of region III, which is a trapezium. The formula for the area of a trapezium is $A\left( \text{trapezium} \right)=\dfrac{1}{2}\times \left( \text{sum of lengths of parallel sides} \right)\times \left( \text{distance between the parallel lines} \right)$.
In region III, we can see that the lengths of the parallel sides are 6 cm and 10 cm. The distance between these two parallel lines is given to be 4 cm. Substituting these values in the formula for the area of trapezium, we get
$\begin{align}
  & \text{Area of region III = }\dfrac{1}{2}\times \left( 10+6 \right)\times 4 \\
 & =16\times 2 \\
 & =32
\end{align}$
Now, to find the area of the given figure, we will add the areas of all the regions as follows,
$\begin{align}
  & \text{Area of given figure = Area of region I +Area of region II + Area of region III } \\
 & \text{+ Area of region IV + Area of region V}
\end{align}$
Substituting the values for the areas that we have calculated, we get
$\begin{align}
  & \text{Area of the given figure = }3\sqrt{91}+60+32+24+24 \\
 & =140+3\sqrt{91}
\end{align}$
Hence, the area of the given figure is $140+3\sqrt{91}$ sq cm.

Note: In this type of question, the key aspect is to use the correct formula to find the areas of the smaller regions. As we are using multiple formulae, it is possible that there is a chance of making minor mistakes in the calculations. So, it is useful to explicitly calculate the area of each region. We should also be able to find the required measurements for the calculations using the given information like we found the altitude for the region I.