Question

Find the area of the minor segment of a circle of radius 14cm, when its central angle is ${60^0}$.Also find the area of the corresponding major segment. $\left[ {use{\text{ }}\pi {\text{ = }}\dfrac{{22}}{7}} \right]$

Answer 1

Hint-Simply use formulae of area of segment. This is the case of a circular segment which is cut off from the rest of the circle.

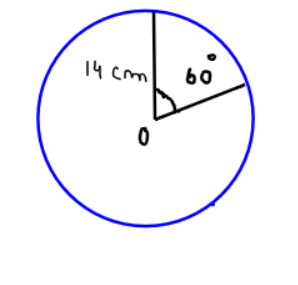
Now it has been given that the radius of the circle is 14cm and the central angle of the minor segment is ${60^0}$.
Now using the formulae that area of segment = $\pi {r^2}\left( {\dfrac{c}{{360}}} \right)$ where c is the central angle of segment
Area of minor segment = $\dfrac{{22}}{7} \times {(14)^2} \times \dfrac{{60}}{{360}}$
$ \Rightarrow \dfrac{{22 \times 2 \times 14}}{6} = 102.67c{m^2}$
Area of minor segment + area of major segment =Total area of the circle…………………….. (1)
Total area of circle $ = \pi {r^2}$
$ \Rightarrow \dfrac{{22}}{7} \times {\left( {14} \right)^2} = 22 \times 2 \times 14 = 616c{m^2}$
Using equation (1) area of major segment is
Total area of circle – area of minor segment
$ \Rightarrow 616 - 102.67 = 513.33c{m^2}$

Note – Whenever we face such problems the key concept is having the basic understanding of the formula for the area of segment when the central angle corresponding to a segment is given.