
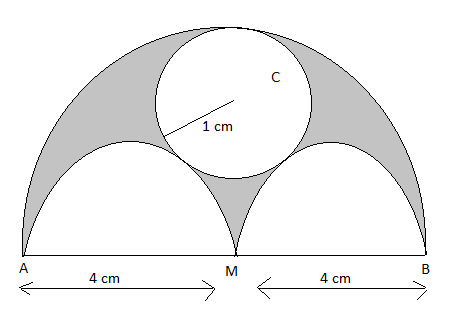
Find the area of the shaded region.

Answer
511.5k+ views
Hint: To find the area of the shaded region in the given figure we will subtract the area of the circle having radius 1 cm and the two semi-circle having radius 2 cm from the bigger semi-circle of radius 4 cm. Then we will get the area of the shaded region.
Complete step-by-step answer:
We have been given the figure as follows:
From the given figure, we can say that the area of the shaded region is equal to the area obtained by subtracting the area of the circle with C as center and the two semi-circles with AM and MB as diameter from the bigger semi-circle having AB as diameter.
We know that area of a circle having D as diameter is as follows:
Area
So, area of semi-circle
Now the area of semi-circle having AM = 4 cm as diameter
Area of semi-circle having MB = 4 cm as diameter
Area of circle having C as center and diameter
Area of semicircle having AB = 8 cm as diameter
So the area of the shaded region = area of semi-circle having AB as diameter – (area of the circle having C as center + 2 area of semi-circle with AM as diameter)
Also,
Area of shaded region
Therefore, the area of the shaded region is
Note: Be careful while calculating the area as we have been given the diameter of some circle and radius of a circle so accordingly use the formula to calculate the area.
Complete step-by-step answer:
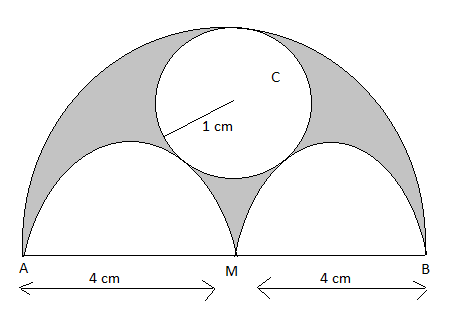
We have been given the figure as follows:

From the given figure, we can say that the area of the shaded region is equal to the area obtained by subtracting the area of the circle with C as center and the two semi-circles with AM and MB as diameter from the bigger semi-circle having AB as diameter.
We know that area of a circle having D as diameter is as follows:
Area
So, area of semi-circle
Now the area of semi-circle having AM = 4 cm as diameter
Area of semi-circle having MB = 4 cm as diameter
Area of circle having C as center and diameter
Area of semicircle having AB = 8 cm as diameter
So the area of the shaded region = area of semi-circle having AB as diameter – (area of the circle having C as center + 2 area of semi-circle with AM as diameter)
Also,
Area of shaded region
Therefore, the area of the shaded region is
Note: Be careful while calculating the area as we have been given the diameter of some circle and radius of a circle so accordingly use the formula to calculate the area.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What are the public facilities provided by the government? Also explain each facility




