
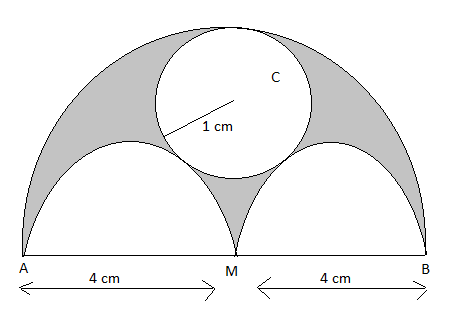
Find the area of the shaded region.

Answer
591.9k+ views
Hint: To find the area of the shaded region in the given figure we will subtract the area of the circle having radius 1 cm and the two semi-circle having radius 2 cm from the bigger semi-circle of radius 4 cm. Then we will get the area of the shaded region.
Complete step-by-step answer:
We have been given the figure as follows:
From the given figure, we can say that the area of the shaded region is equal to the area obtained by subtracting the area of the circle with C as center and the two semi-circles with AM and MB as diameter from the bigger semi-circle having AB as diameter.
We know that area of a circle having D as diameter is as follows:
Area \[=\dfrac{\pi {{D}^{2}}}{4}\]
So, area of semi-circle \[=\dfrac{1}{2}\times \] area of circle
\[\begin{align}
& =\dfrac{1}{2}\times \dfrac{\pi {{D}^{2}}}{4} \\
& =\dfrac{\pi {{D}^{2}}}{8} \\
\end{align}\]
Now the area of semi-circle having AM = 4 cm as diameter \[=\dfrac{\pi {{D}^{2}}}{8}\]
\[=\dfrac{\pi \times {{\left( 4 \right)}^{2}}}{8}=\dfrac{\pi \times 16}{8}=2\pi c{{m}^{2}}\]
Area of semi-circle having MB = 4 cm as diameter \[=\dfrac{\pi {{D}^{2}}}{8}\]
\[=\dfrac{\pi \times 4}{8}=\dfrac{\pi \times 16}{8}=2\pi c{{m}^{2}}\]
Area of circle having C as center and diameter \[=\left( 2\times 1 \right)cm\] is \[=\dfrac{\pi {{D}^{2}}}{4}\]
\[=\dfrac{\pi \times {{\left( 2 \right)}^{2}}}{4}=\pi c{{m}^{2}}\]
Area of semicircle having AB = 8 cm as diameter \[=\dfrac{\pi {{D}^{2}}}{8}\]
\[=\dfrac{\pi \times {{8}^{2}}}{8}=\pi \times 8=8\pi c{{m}^{2}}\]
So the area of the shaded region = area of semi-circle having AB as diameter – (area of the circle having C as center + 2 area of semi-circle with AM as diameter)
\[=8\pi -\left( \pi +2\times 2\pi \right)=8\pi -5\pi =3\pi c{{m}^{2}}\]
Also, \[\pi =\dfrac{22}{7}\] so by substituting the value of \[\pi \] we get as follows:
Area of shaded region \[=3\pi =3\times \dfrac{22}{7}=9.43c{{m}^{2}}(approx)\]
Therefore, the area of the shaded region is \[9.43c{{m}^{2}}(approx)\].
Note: Be careful while calculating the area as we have been given the diameter of some circle and radius of a circle so accordingly use the formula to calculate the area.
Complete step-by-step answer:
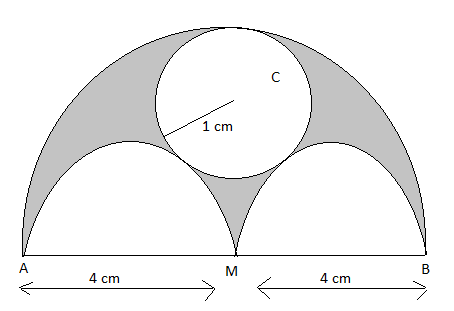
We have been given the figure as follows:

From the given figure, we can say that the area of the shaded region is equal to the area obtained by subtracting the area of the circle with C as center and the two semi-circles with AM and MB as diameter from the bigger semi-circle having AB as diameter.
We know that area of a circle having D as diameter is as follows:
Area \[=\dfrac{\pi {{D}^{2}}}{4}\]
So, area of semi-circle \[=\dfrac{1}{2}\times \] area of circle
\[\begin{align}
& =\dfrac{1}{2}\times \dfrac{\pi {{D}^{2}}}{4} \\
& =\dfrac{\pi {{D}^{2}}}{8} \\
\end{align}\]
Now the area of semi-circle having AM = 4 cm as diameter \[=\dfrac{\pi {{D}^{2}}}{8}\]
\[=\dfrac{\pi \times {{\left( 4 \right)}^{2}}}{8}=\dfrac{\pi \times 16}{8}=2\pi c{{m}^{2}}\]
Area of semi-circle having MB = 4 cm as diameter \[=\dfrac{\pi {{D}^{2}}}{8}\]
\[=\dfrac{\pi \times 4}{8}=\dfrac{\pi \times 16}{8}=2\pi c{{m}^{2}}\]
Area of circle having C as center and diameter \[=\left( 2\times 1 \right)cm\] is \[=\dfrac{\pi {{D}^{2}}}{4}\]
\[=\dfrac{\pi \times {{\left( 2 \right)}^{2}}}{4}=\pi c{{m}^{2}}\]
Area of semicircle having AB = 8 cm as diameter \[=\dfrac{\pi {{D}^{2}}}{8}\]
\[=\dfrac{\pi \times {{8}^{2}}}{8}=\pi \times 8=8\pi c{{m}^{2}}\]
So the area of the shaded region = area of semi-circle having AB as diameter – (area of the circle having C as center + 2 area of semi-circle with AM as diameter)
\[=8\pi -\left( \pi +2\times 2\pi \right)=8\pi -5\pi =3\pi c{{m}^{2}}\]
Also, \[\pi =\dfrac{22}{7}\] so by substituting the value of \[\pi \] we get as follows:
Area of shaded region \[=3\pi =3\times \dfrac{22}{7}=9.43c{{m}^{2}}(approx)\]
Therefore, the area of the shaded region is \[9.43c{{m}^{2}}(approx)\].
Note: Be careful while calculating the area as we have been given the diameter of some circle and radius of a circle so accordingly use the formula to calculate the area.
Recently Updated Pages
What happens to glucose which enters nephron along class 10 biology CBSE

Write a dialogue with at least ten utterances between class 10 english CBSE

A circle is inscribed in an equilateral triangle and class 10 maths CBSE

When the JanmiKudian Act was passed that granted the class 10 social science CBSE

A sector containing an angle of 120 circ is cut off class 10 maths CBSE

The sum of digits of a two digit number is 13 If t-class-10-maths-ICSE

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the missing number in the sequence 259142027 class 10 maths CBSE




