Question

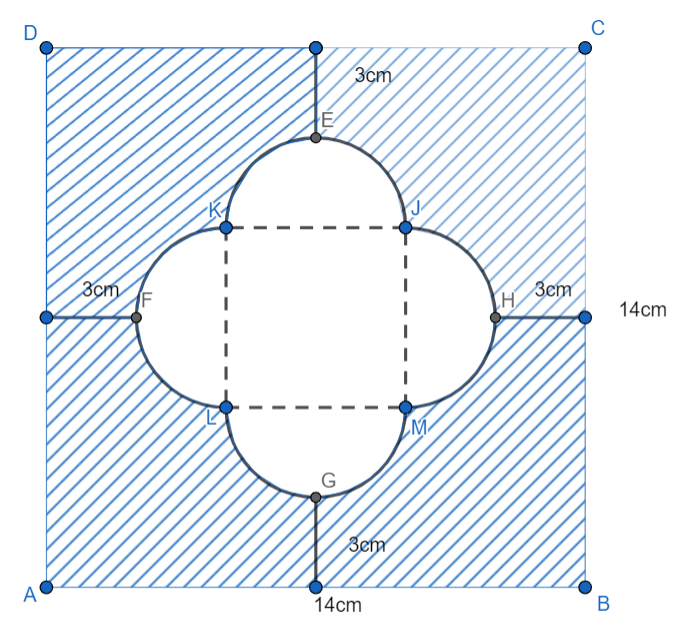
Find the area of the shaded region given in figure.

Answer 1

Hint: We will find the total area of the larger square $(ABCD)$ using the formula area of square$={{(side)}^{2}}$. Then we will find the area of the smaller square $(JKLM)$ using the same formula and then we will find the area of any one semicircle and multiply it by $4$, as given in the above figure.

Complete step-by-step answer:
Finally we will subtract the area of the smaller square $(JKLM)$+$4$ $Semicircles$ from larger square to get the area of shaded or hatched region.

The figure given in the question is that $ABCD$ is a square of side $14cm$. Also, we have a smaller square $JKLM$ inside the larger square and four semicircles.

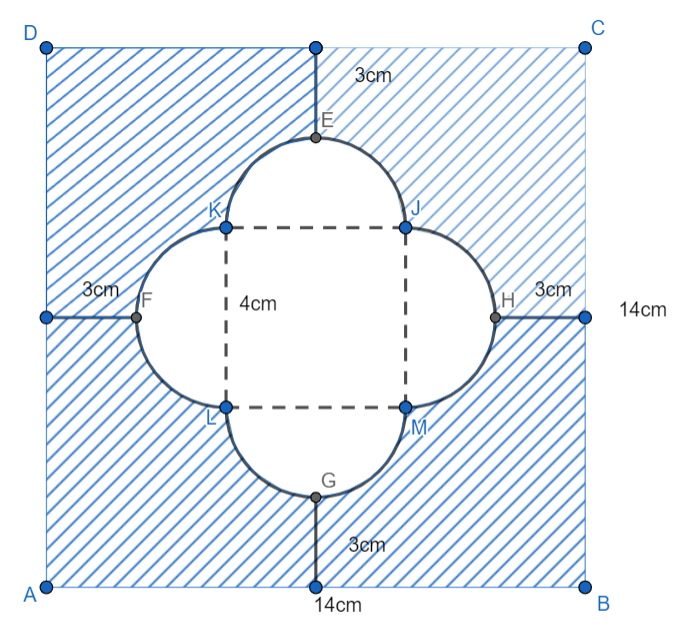
From the above figure, we can consider the distribution of small squares and semicircles as shown below.

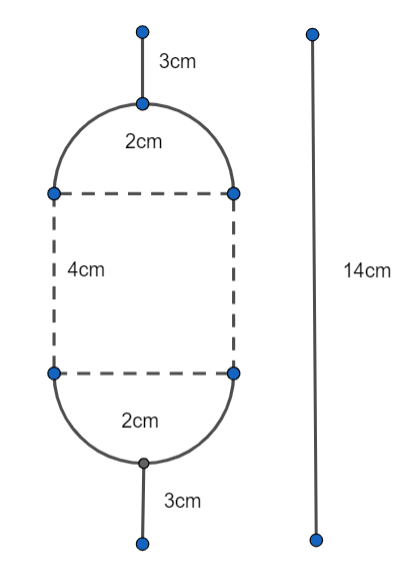
From the above figure we get side of square $JKLM=4cm$ and the diameter of the circle is also $4cm$

We will first find the area of the larger square $ABCD$ measuring side as $14cm$.

Using formula for area of square$={{(side)}^{2}}$, we can substitute side$=14cm$.

$\begin{align}
& ={{(14cm)}^{2}} \\
& =196c{{m}^{2}} \\
\end{align}$

Now, we will calculate the area of smaller square $JKLM$

Using formula for area of square\[=\text{ }{{\left( Side \right)}^{2}}\], we can substitute side$=4cm$.

$\begin{align}
& ={{(4cm)}^{2}} \\
& =16c{{m}^{2}} \\
\end{align}$

Now, calculate the area of semicircles having radius $2cm$. As we know that area of circle is given by $\pi {{r}^{2}}$, from this we get area of one semicircle =$\dfrac{\pi {{r}^{2}}}{2}$.

On substituting the value of $r=2cm$, we get

Area of one semicircle $=\dfrac{\pi \times {{2}^{2}}}{2}$

$\begin{align}
& =\dfrac{\pi \times 4}{2} \\
& =2\pi c{{m}^{2}} \\
\end{align}$

But, we have $4$ semicircles in the figure. Using unitary method,

Area of $4$ semicircles will be $=4(2\times \pi )c{{m}^{2}}$=$ 8 \pi cm^2$

We know that the value of $\pi $ is $3.14$. Substituting the value of $\pi $ in the above value

\[=8\times 3.14c{{m}^{2}}\]

$=25.12c{{m}^{2}}$

Now, we have all the required values to find the area of the shaded region.

The area of shaded region is given by,

{(Area of square $ABCD$)$-$(Area of square $JKLM$)$+$(Area of $4$ semicircles)}

We have,

Area of square $ABCD$=$196c{{m}^{2}}$

Area of square $JKLM$=$16c{{m}^{2}}$

Area of $4$ semicircles $=25.12c{{m}^{2}}$

Substituting the above values in formula,

Area of shaded region \[=\text{ }196c{{m}^{2}}-(\text{ }\left( 16c{{m}^{2}} \right)\text{ }+\text{ }\left( 25.12c{{m}^{2}} \right))\]
Apply BODMAS rule, we get

$\begin{align}
& =196c{{m}^{2}}-41.12c{{m}^{2}} \\
& =154.88c{{m}^{2}} \\
\end{align}$
Thus, the area of the shaded region is $154.88c{{m}^{2}}$.

Note: You can find the area of $4$ semicircles of the same radius using the direct formula of area of circle multiplying by $2$. As $4$ semicircles of equal radius will form two complete circles. Thus, you can use $2\times \pi {{r}^{2}}$ to find the area of $4$ semicircles. In question we have $4$ semicircles of equal radius.
\[\begin{align}
& Area\text{ }of\text{ }4\text{ }semicircles\text{ }=2\times \pi {{r}^{2}} \\
& =2\times 3.14\times {{2}^{2}} \\
& =8\times 3.14 \\
& =25.12c{{m}^{2}}. \\
\end{align}\]