Question

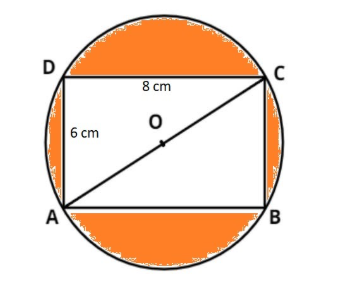
Find the area of the shaded region if ABCD is a rectangle with sides 8 cm and 6 cm and O is the center of the circle. (Take $\pi = 3.14$)

Answer 1

Hint: As we can see a rectangle is inside the circle. Now the area of the shaded region can be calculated by subtracting the area of the rectangle from the area of the circle.

Complete step-by-step answer:
Given,
ABCD is a rectangle with sides AD=6 cm and DC=8 cm
Therefore,
Area of rectangle$ = AD \times DC = 6 \times 8 = 48{\text{ c}}{{\text{m}}^2}$
Now, it is given that O is the center of the circle as AC is the diameter of the circle.
From figure $\vartriangle ADC$ is a right angle triangle.
$
   \Rightarrow A{C^2} = A{D^2} + D{C^2} \\
   \Rightarrow A{C^2} = {6^2} + {8^2} = 100 \\
   \Rightarrow AC = 10 \\
$
Therefore, radius of circle is OC(r)$ = \dfrac{{AC}}{2} = 5$
Now, Area of circle$ = \pi {r^2} = 3.14 \times {5^2} = 78.5{\text{ c}}{{\text{m}}^2}$
Therefore,
Area of shaded region = Area of circle –Area of rectangle
                                        $
   = 78.5 - 48 \\
   = 30.5{\text{ c}}{{\text{m}}^2} \\
$
So this is your desired answer.

Note: In this type of question first calculate the area of all the shapes given, then subtract the unwanted area, and always remember the area formulas of all standard shapes.