Question

Find the area of the triangle whose vertices are A (-3,-1), B (5,3), C (2,-8)
A. 34
B. 36
C. 38
D. 32

Answer 1

Hint: We use the formula to find the area of a triangle when coordinates of vertices are given. The formula has been derived by finding the length of the base of the triangle and its height using the distance formula. Drawing the triangle also helps to understand the problem better.

Complete step-by-step answer:
We will first sketch the given triangle.

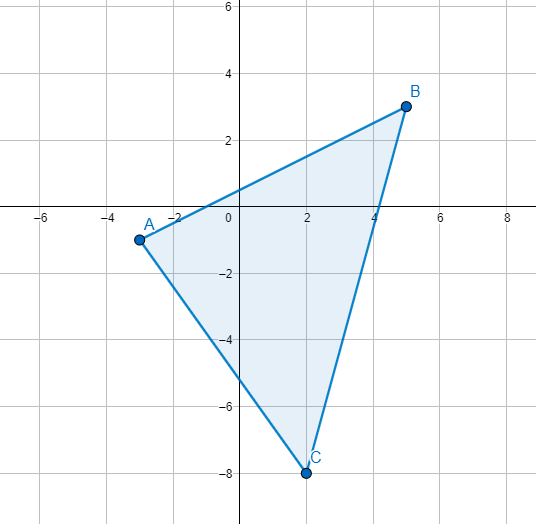
Let us label the vertex A as $A\left( {{A}_{X}},{{A}_{Y}} \right)=\left( -3,-1 \right)$ .
Label vertex B as $B\left( {{B}_{X}},{{B}_{Y}} \right)=\left( 5,3 \right)$.
Label vertex C as $C\left( {{C}_{X}},{{C}_{Y}} \right)=\left( 2,-8 \right)$.
Given the coordinates of the vertices, the area of the triangle is given by the formula:
\[\left| \dfrac{{{A}_{X}}\left( {{B}_{Y}}-{{C}_{Y}} \right)+{{B}_{X}}\left( {{C}_{Y}}-{{A}_{Y}} \right)+{{C}_{X}}\left( {{A}_{Y}}-{{B}_{Y}} \right)}{2} \right|\]
Substituting the values of the vertices, we get,
\[\begin{align}
  & \left| \dfrac{-3\left( 3-(-8) \right)+5\left( -8-(-1) \right)+2\left( -1-3 \right)}{2} \right| \\
 & \\
 & =\left| \dfrac{-3\left( 11 \right)+5\left( -7 \right)+2\left( -4 \right)}{2} \right| \\
 & \\
 & =\left| \dfrac{-33+(-35)+(-8)}{2} \right| \\
 & \\
 & =\left| \dfrac{-76}{2} \right| \\
 & \\
 & =38 \\
\end{align}\]

Thus, option C is the correct option.

Note: There is a chance of making a mistake while using the formula of the area of the triangle. The coordinates of each vertex must be noted properly. An alternate method is to use Heron’s formula to find the area. In this method we will first need to find the lengths of all the sides of the triangle. This can be done using distance formula. After that we find the semi perimeter of the triangle, which is half of the perimeter of the triangle. Afterwards, we substitute this in Heron’s formula.
If the lengths of the sides are a, b and c respectively, then the semi perimeter S is given by
$S=\left( \dfrac{a+b+c}{2} \right)$ .
The area A is given by:
$A=\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}$ .
While using Heron's formula, we must make sure we substitute the proper values in the formula. One must also watch out for any calculation mistakes while using the formula as square root is involved.