Question

Find the area of the triangle with 5cm, 12cm, 13cm.

Answer 1

Hint: We need to find which kind of triangle it is. We can check if the triangle is right angle triangle or not by checking the Pythagoras theorem. The Pythagoras theorem says that ${{\left( \text{Hypotenuse} \right)}^{\text{2}}}\text{=}{{\left( \text{Base} \right)}^{\text{2}}}\text{+}{{\left( \text{Height} \right)}^{\text{2}}}$ . The hypotenuse is always the biggest side in the triangle.

Complete step-by-step answer:
If the triangle is right angle triangle then the area of the triangle is given by $A=\dfrac{1}{2}\times \text{Base }\!\!\times\!\!\text{ Height}$ .

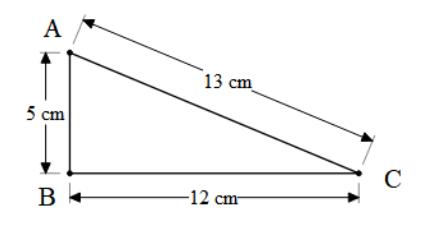
We need to find the area of this triangle.
Let’s assume the triangle ABC with sides AB = 5cm, BC = 12cm, and AC = 13 cm.
Let’s first check whether the triangle is right angle triangle or not.
We can check this with the help of the Pythagoras theorem.
The Pythagoras theorem is only applicable for the right-angle triangle.
Therefore, if the Pythagoras theorem is satisfied then we can say that the triangle is right-angled.
The Pythagoras theorem says that ${{\left( \text{Hypotenuse} \right)}^{\text{2}}}\text{=}{{\left( \text{Base} \right)}^{\text{2}}}\text{+}{{\left( \text{Height} \right)}^{\text{2}}}$ .
The hypotenuse is always the biggest side in the triangle.
Substituting the values, we get,
$\begin{align}
  & {{\left( 13 \right)}^{2}}={{\left( 5 \right)}^{2}}+{{\left( 12 \right)}^{2}} \\
 & 169=25+144 \\
 & 169=169 \\
\end{align}$
Thus, we can see that equality holds that means that the triangle ABC is right-angled.
As we can see that, $\angle ABC={{90}^{\circ }}$ ,
Therefore, the area of the right-angle triangle (A) is given by,
$A=\dfrac{1}{2}\times \text{Base }\!\!\times\!\!\text{ Height}........\text{(i)}$
We can say that Height = AB = 5cm and Base = BC = 12cm.
Substituting the value in equation (i), we get,
$\begin{align}
  & A=\dfrac{1}{2}\times 5\times 12 \\
 & =5\times 6 \\
 & =30c{{m}^{2}}
\end{align}$
Therefore, the area of the triangle with sides 5cm, 12cm, 13cm is $30c{{m}^{2}}$.

Note: The calculation of the area of the right-angle triangle is easiest. In other cases, we need to drop the perpendicular on the base of the triangle and then calculate the area. In the right-angle triangle, one side is already perpendicular to one of the sides. We can also see that the 5, 12, 13 is a Pythagorean triplet, the other Pythagorean triplets are 3, 4, 5. This means that any triangle with sides of Pythagorean triplets is always a right angle triangle.