
How do you find the asymptote(s) or hole(s) of $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$ ?
Answer
550.8k+ views
Hint: First make sure the rational function is written in simplified (reduced) form.
Then, look for values that cause the denominator to be zero (and numerator to be zero); that is, we solve $d\left( c \right) = 0$ , where $d\left( x \right)$ is the denominator of $f\left( x \right)$ , and then evaluate $\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right)$ and $\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right)$ to ascertain the behavior of the function at $x = c$ .
To find the horizontal asymptotes we compute $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$ and $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$ .
If $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L$ or $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L$ , then the line $y = L$ is a horizontal asymptote of the graph of $f$ .
Formula used: The line $x = c$ is a vertical asymptote of the graph of $f$ if either of the one-sided limits $\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right)$ or $\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right)$ is infinite.
The line $y = L$ is a horizontal asymptote of the graph of $f$ if
$\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L$ or $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L$
Complete step-by-step solution:
First make sure the rational function is written in simplified (reduced) form.
Because vertical asymptote for $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$ occur at values of $c$ for which $\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right)$ or $\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right)$ is infinite, we look for values that cause the denominator to be zero (and numerator to be zero); that is, we solve $d\left( c \right) = 0$, where $d\left( x \right)$ is the denominator of $f\left( x \right)$, and then evaluate $\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right)$ and $\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right)$ to ascertain the behavior of the function at $x = c$.
To find the horizontal asymptotes we compute $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$ and $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$. If $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L$ or $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L$, then the line $y = L$ is a horizontal asymptote of the graph of $f$.
Now, consider $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$
We have to find its asymptote.
We can simplify the function using identity ${a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)$.
Denominator can be simplified using this identity by putting $a = x$ and $b = 3$.
So, putting $a = x$ and $b = 3$in ${a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)$.
$ \Rightarrow {x^2} - 9 = \left( {x - 3} \right)\left( {x + 3} \right)$
Now, putting this simplified version of ${x^2} - 9$ in $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$.
$ \Rightarrow f\left( x \right) = \dfrac{{x + 3}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}$
Cancel out $\left( {x + 3} \right)$ from numerator and denominator.
$ \Rightarrow f\left( x \right) = \dfrac{1}{{x - 3}}$
Vertical Asymptotes:
We know that vertical asymptotes are found by setting the denominator equal to zero, because this is the value for which the function is undefined.
So, putting $x - 3 = 0$, to find vertical asymptotes of given function.
Thus, $x = 3$ is the value that causes division by zero, so we find $\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right)$ and $\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right)$ to ascertain the behavior of the function at $x = 3$.
Putting $f\left( x \right) = \dfrac{1}{{x - 3}}$in $\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right)$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{1}{{x - 3}} = + \infty $
Putting $f\left( x \right) = \dfrac{1}{{x - 3}}$in $\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right)$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{1}{{x - 3}} = - \infty $
This means that $x = 3$ is a vertical asymptote and the graph is moving downward as $x \to 3$ from the left and upward as $x \to 3$ from the right.
Horizontal Asymptotes:
To find the horizontal asymptotes we compute $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$ and $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$.
Putting $f\left( x \right) = \dfrac{1}{{x - 3}}$in $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{x - 3}}$
Dividing numerator and denominator by $x$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{x - 3}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\dfrac{1}{x}}}{{1 - \dfrac{3}{x}}}$
Now, by direct substituting and using $\dfrac{1}{\infty } = 0$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{x - 3}} = 0$
Putting $f\left( x \right) = \dfrac{1}{{x - 3}}$in $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{x - 3}}$
Dividing numerator and denominator by $x$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{x - 3}} = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{1}{x}}}{{1 - \dfrac{3}{x}}}$
Now, by direct substituting and using $\dfrac{1}{\infty } = 0$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{x - 3}} = 0$
So, $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0$ and $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 0$.
Thus, $y = 0$ is a horizontal asymptote.
Therefore, $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$ has vertical asymptote at $x = 3$ and horizontal asymptote at $y = 0$.
Note: We can also find the horizontal and vertical asymptotes by looking at the graph of function
$ \Rightarrow f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$.
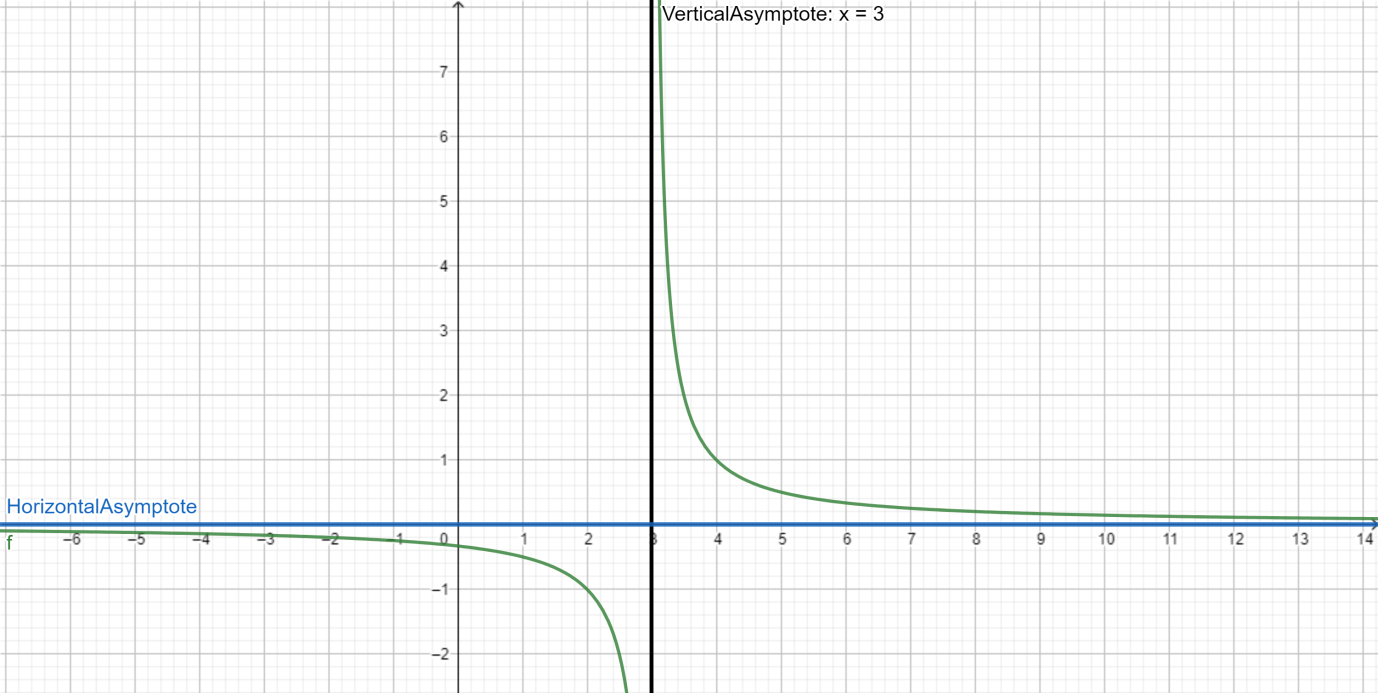
Therefore, $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$ has vertical asymptote at $x = 3$ and horizontal asymptote at $y = 0$.
Then, look for values that cause the denominator to be zero (and numerator to be zero); that is, we solve $d\left( c \right) = 0$ , where $d\left( x \right)$ is the denominator of $f\left( x \right)$ , and then evaluate $\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right)$ and $\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right)$ to ascertain the behavior of the function at $x = c$ .
To find the horizontal asymptotes we compute $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$ and $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$ .
If $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L$ or $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L$ , then the line $y = L$ is a horizontal asymptote of the graph of $f$ .
Formula used: The line $x = c$ is a vertical asymptote of the graph of $f$ if either of the one-sided limits $\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right)$ or $\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right)$ is infinite.
The line $y = L$ is a horizontal asymptote of the graph of $f$ if
$\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L$ or $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L$
Complete step-by-step solution:
First make sure the rational function is written in simplified (reduced) form.
Because vertical asymptote for $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$ occur at values of $c$ for which $\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right)$ or $\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right)$ is infinite, we look for values that cause the denominator to be zero (and numerator to be zero); that is, we solve $d\left( c \right) = 0$, where $d\left( x \right)$ is the denominator of $f\left( x \right)$, and then evaluate $\mathop {\lim }\limits_{x \to {c^ - }} f\left( x \right)$ and $\mathop {\lim }\limits_{x \to {c^ + }} f\left( x \right)$ to ascertain the behavior of the function at $x = c$.
To find the horizontal asymptotes we compute $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$ and $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$. If $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L$ or $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L$, then the line $y = L$ is a horizontal asymptote of the graph of $f$.
Now, consider $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$
We have to find its asymptote.
We can simplify the function using identity ${a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)$.
Denominator can be simplified using this identity by putting $a = x$ and $b = 3$.
So, putting $a = x$ and $b = 3$in ${a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)$.
$ \Rightarrow {x^2} - 9 = \left( {x - 3} \right)\left( {x + 3} \right)$
Now, putting this simplified version of ${x^2} - 9$ in $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$.
$ \Rightarrow f\left( x \right) = \dfrac{{x + 3}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}$
Cancel out $\left( {x + 3} \right)$ from numerator and denominator.
$ \Rightarrow f\left( x \right) = \dfrac{1}{{x - 3}}$
Vertical Asymptotes:
We know that vertical asymptotes are found by setting the denominator equal to zero, because this is the value for which the function is undefined.
So, putting $x - 3 = 0$, to find vertical asymptotes of given function.
Thus, $x = 3$ is the value that causes division by zero, so we find $\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right)$ and $\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right)$ to ascertain the behavior of the function at $x = 3$.
Putting $f\left( x \right) = \dfrac{1}{{x - 3}}$in $\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right)$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{1}{{x - 3}} = + \infty $
Putting $f\left( x \right) = \dfrac{1}{{x - 3}}$in $\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right)$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to {3^ - }} \dfrac{1}{{x - 3}} = - \infty $
This means that $x = 3$ is a vertical asymptote and the graph is moving downward as $x \to 3$ from the left and upward as $x \to 3$ from the right.
Horizontal Asymptotes:
To find the horizontal asymptotes we compute $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$ and $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$.
Putting $f\left( x \right) = \dfrac{1}{{x - 3}}$in $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{x - 3}}$
Dividing numerator and denominator by $x$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{x - 3}} = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\dfrac{1}{x}}}{{1 - \dfrac{3}{x}}}$
Now, by direct substituting and using $\dfrac{1}{\infty } = 0$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{x - 3}} = 0$
Putting $f\left( x \right) = \dfrac{1}{{x - 3}}$in $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{x - 3}}$
Dividing numerator and denominator by $x$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{x - 3}} = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{1}{x}}}{{1 - \dfrac{3}{x}}}$
Now, by direct substituting and using $\dfrac{1}{\infty } = 0$, we get
$ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{x - 3}} = 0$
So, $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0$ and $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 0$.
Thus, $y = 0$ is a horizontal asymptote.
Therefore, $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$ has vertical asymptote at $x = 3$ and horizontal asymptote at $y = 0$.
Note: We can also find the horizontal and vertical asymptotes by looking at the graph of function
$ \Rightarrow f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$.

Therefore, $f\left( x \right) = \dfrac{{x + 3}}{{{x^2} - 9}}$ has vertical asymptote at $x = 3$ and horizontal asymptote at $y = 0$.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




