Question

Find the breadth of the rectangle whose length is 70 cm and perimeter 200 cm.

Answer 1

Hint: We had to only assume the breadth of the rectangle and then apply the perimeter formula for a rectangle which is perimeter = 2(length + breadth).

Complete step-by-step answer:

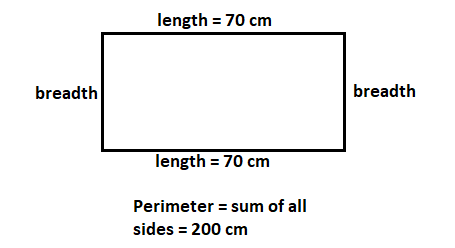
As we know that we are given with the perimeter of the rectangle that is 70 cm.
And according to the perimeter of any shape, perimeter is the sum of its all sides, or we can say that it is the length of the boundaries of the shape.
A rectangle is a 2D shape whose opposite sides are of equal lengths. And whose diagonal lengths are equal.
And diagonal is the line formed by joining two opposite vertices of the rectangle.
And the length and breadth of the rectangle are its two adjacent sides.
So, the perimeter of the rectangle should be = length + breadth + length + breadth = 2(length + breadth)
So, let us draw the rectangle whose length and perimeter are given.

So, let the breadth of the rectangle be = x cm.
So, 200 = 2(70 + x) =140 + 2x
Subtracting 2x from both the sides of the above equation. We get,
70 = 2x
On dividing both sides of the above equation by 2. We get,
x = 35 cm
Hence, the breadth of the rectangle whose perimeter is 200cm and length is 70 cm will be 35 cm.

Note: Whenever we come up with this type of question then we should remember that the perimeter of any shape (figure) is the sum of the length of all its sides. And there are four sides in a rectangle out of which opposite sides are equal and adjacent sides are different. And the adjacent sides of the rectangle are known as length and breadth. So, the formula for the perimeter of the rectangle is 2(length + breadth). So, we assume the breadth of the rectangle as x and put the value of length and breadth of the rectangle in the formula and equate that with the given perimeter to get the required value of breadth of the rectangle.